题目内容
【题目】已知函数f（x）=Asin（ωx+ 
）（A＞0，ω＞0）的图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0 ， 2）和（x0+ 
，﹣2）．
（1）求函数f（x）的解析式；
（2）求sin（x0+ 
）的值．
【答案】
（1）解：∵图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0，2）和（x0+ 
，﹣2）．
∴A=2， 
=x0+ ﹣x0= ，
即函数的周期T=π，即T= 
，解得ω=2，
即f（x）=2sin（2x+ 
）
（2）解：∵函数的最高点的坐标为（x0，2），
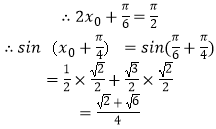
∴2x0+ = ，
即x0= ，
则sin（x0+ 
）=sin（ + ）=sin cos +cos sin
= 
（sin +cos ）= （ 
）= 
【解析】（1）根据条件求出振幅以及函数的周期，即可求函数f（x）的解析式；（2）根据函数的最值，求出x0的大小，结合两角和差的正弦公式进行求解即可．
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：
．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
