题目内容
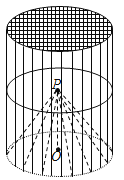
【题目】如图,圆锥的轴截面为等腰![]() 为底面圆周上一点。
为底面圆周上一点。
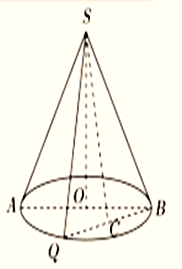
(1)若![]() 的中点为
的中点为![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)如果![]() ,求此圆锥的体积;
,求此圆锥的体积;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() .
.
【答案】(1)证明见解析(2)![]() (3)60°
(3)60°
【解析】
(1)连接![]() 、
、![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() ,由圆周角定理我们可得
,由圆周角定理我们可得![]() ,由圆锥的几何特征,可得
,由圆锥的几何特征,可得![]() ,进而由线面垂直的判定定理,得到
,进而由线面垂直的判定定理,得到![]() 平面
平面![]() ,则
,则![]() ,结合
,结合![]() 及线面垂直的判定定理得到
及线面垂直的判定定理得到![]() 平面
平面![]() ;
;
(2)若![]() ,易得
,易得![]() ,又由
,又由![]() ,我们求出圆锥的底面半径
,我们求出圆锥的底面半径![]() 长及圆锥的高
长及圆锥的高![]() ,代入圆锥体积公式,即可得到圆锥的体积;
,代入圆锥体积公式,即可得到圆锥的体积;
(3)作![]() 于点
于点![]() ,由面面垂直的判定定理可得
,由面面垂直的判定定理可得![]() 平面
平面![]() ,作
,作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,根据二面角
的平面角,根据二面角![]() 的大小为
的大小为![]() ,设
,设![]() ,
,![]() ,进而可求出
,进而可求出![]() 的大小
的大小
(1)如图:
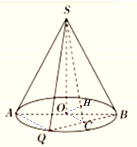
连接![]() 、
、![]() ,因为
,因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() 为圆的直径,所以
为圆的直径,所以![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() .又
.又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)![]()
![]() ,
,![]()
![]() ,
,![]() ,又
,又![]() ,
,![]()
![]() ,
,![]() .
.
(3)作![]() 于点
于点![]() ,
,![]() 平面
平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]()
![]() 平面
平面![]() .再作
.再作![]() 于点
于点![]() ,连
,连![]() ,
,![]()
![]() 为二面角
为二面角![]() 的平面角
的平面角
如图:
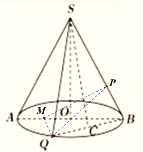
![]() ,
,![]() .
.
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.![]()
![]()
![]() ,解得
,解得![]() ,
,![]()

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目