题目内容
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A、B,且
的左焦点为F,短轴的两个端点分别为A、B,且![]() ,
,![]() 为等边三角形.
为等边三角形.
(1)求椭圆C的方程;
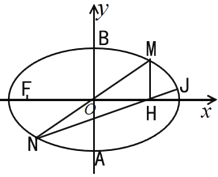
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与椭圆C交于另一点R;求
与椭圆C交于另一点R;求![]() 面积取最大值时,直线
面积取最大值时,直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() .(也可写成
.(也可写成![]() .)
.)
【解析】
(1)由椭圆左焦点为F,短轴的两个端点分别为A、B,且![]() ,
,![]() 为等边三角形,列出方程组,求出a,b,由此能求出椭圆C的方程.
为等边三角形,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)设![]() ,则由条件,知
,则由条件,知![]() ,
,![]() ,且
,且![]() ,
,![]() .推导出
.推导出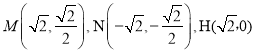 ,进而求得直线NH的方程:
,进而求得直线NH的方程:![]() .由
.由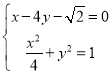 求得
求得![]() .再求出线段
.再求出线段![]() 的中点坐标,由此能求出以线段
的中点坐标,由此能求出以线段![]() 为直径的圆的方程.
为直径的圆的方程.
(3)当直线![]() 的斜率为0时,
的斜率为0时,![]() .当直线
.当直线![]() 的斜率存在且不为0时,设其方程为
的斜率存在且不为0时,设其方程为![]() ,利用点到直线距离公式、弦长公式、直线垂直、三角形面积公式,结合已知条件能求出结果.
,利用点到直线距离公式、弦长公式、直线垂直、三角形面积公式,结合已知条件能求出结果.
(1)∵椭圆![]() 的左焦点为F,短轴的两个端点分别为A、B
的左焦点为F,短轴的两个端点分别为A、B
且![]() ,
,![]() 为等边三角形.
为等边三角形.
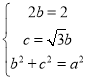 ,解得
,解得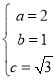 ,∴椭圆C的方程为
,∴椭圆C的方程为(2)设![]() ,则由条件,知
,则由条件,知![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
从而![]() .
.
于是由![]() 及
及![]() ,得
,得![]() .
.
再由点M在椭圆C上,得![]() ,求得
,求得![]() .
.
所以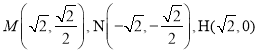 ,
,
进而求得直线NH的方程:![]() .
.
由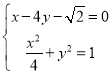 求得
求得![]() .
.
进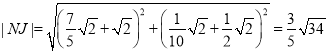 ,
,
线段![]() 的中点坐标为
的中点坐标为![]() .
.
∴以线段![]() 为直径的圆的方程为:
为直径的圆的方程为:![]() .
.
(3)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与椭圆C相切于点A,不合题意,
与椭圆C相切于点A,不合题意,
当直线![]() 的斜率为0时,由题意得
的斜率为0时,由题意得![]() .
.
当直线![]() 的斜率存在且不为0时,设其方程为
的斜率存在且不为0时,设其方程为![]() ,
,
则点O到直线![]() 的距离为
的距离为![]() ,从而由几何意义,得
,从而由几何意义,得![]() ,
,
由于![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,由题意得它与椭圆C的交点R的坐标为
,由题意得它与椭圆C的交点R的坐标为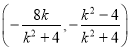 ,
,
于是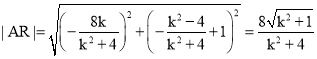 .
.
故![]() ,
,
令![]() ,则
,则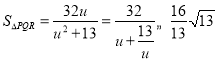 ,
,
当且仅当![]() 即
即![]() 时,上式取等号.
时,上式取等号.
∵![]() ,故当
,故当![]() 时,
时,![]() ,
,
此时直线![]() 的方程为:
的方程为:![]() .(也可写成
.(也可写成![]() .)
.)

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该书每本的成本为![]() 元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: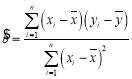
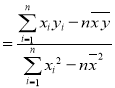 ,
,![]() .
.