题目内容
【题目】已知集合A={x|x2﹣3x﹣10＜0}，B={x|m+1≤x≤2m﹣1}．
（1）当m=3时，求集合（UA）∩B；
（2）若A∩B=B，求实数m的取值范围．
【答案】
（1）解：集合A={x|x2﹣3x﹣10＜0}={x|（x+2）（x﹣5）＜0}
={x|﹣2＜x＜5}，
当m=3时，B={x|4≤x≤5}；
所以RA={x|x≤﹣2或x≥5}；
所以（RA）∩B={x|x=5}={5}；
（2）解：因为A∩B=B，所以BA；
①当B=时，m+1＞2m﹣1，解得m＜2，此时BA；
②当B≠时，应满足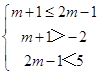 
，
解得2≤m＜3，此时BA；
综上所述，m的取值范围是{m|m＜3}．
【解析】（1）求出A中不等式的解集确定出A，把m的值代入B确定出B，求出A补集与B的交集即可；（2）由题意得到B为A的子集，分B为空集与不为空集两种情况求出m的范围即可．
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案，需要熟知求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析，得到如下数据：
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因，识图能力的一个数据丢失，但已知识图能力样本平均值是5.5．
（Ⅰ）求丢失的数据；
（Ⅱ）经过分析，知道记忆能力x和识图能力y之间具有线性相关关系，请用最小二乘法求出y关于x的线性回归方程 
；
（III）若某一学生记忆能力值为12，请你预测他的识图能力值．