题目内容

(1)
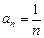
(2)略
(3)(1,+∞)
(1)∵(Sn-1)an-1 = Sn-1 an-1-an,
∴(Sn-Sn-1-1)an-1 =-an,即 anan-1-an-1 + an = 0.
∵ an≠0,若不然,则an-1 = 0,从而与a1 = 1矛盾,∴ anan-1≠0,
∴ anan-1-an-1 + an = 0两边同除以anan-1,得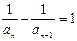 (n≥2).
(n≥2).
又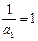 ,∴ {
,∴ {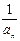 }是以1为首项,1为公差为等差数列,
}是以1为首项,1为公差为等差数列,
则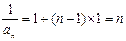 ,
,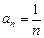 . …………………… 4分
. …………………… 4分
(2)∵ bn =" an2" =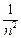 ,∴ 当 n = 1时,Tn =
,∴ 当 n = 1时,Tn = 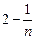 ; …… 5分
; …… 5分
当n≥2时,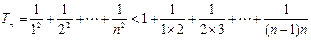
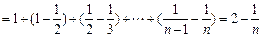 ………… 8分
………… 8分
(3)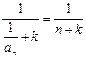 , ∴
, ∴ 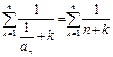 .
.
设 g(n)=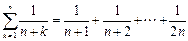 ,
,
∴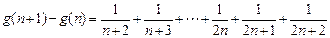
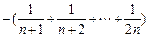
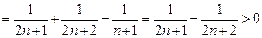 ,
,
∴ g (n)为增函数,
从而 g (n)|min = g(1)=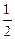 . …………………… 10分
. …………………… 10分
因为 g (n)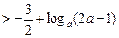 对任意正整数n都成立,
对任意正整数n都成立,
所以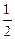
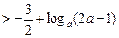 ,得 log a(2a-1)<2,即 log a(2a-1)< log a a2.
,得 log a(2a-1)<2,即 log a(2a-1)< log a a2.
① 当a>1时,有 0<2a-1<a2,解得 a>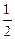 且a≠1,∴ a>1.
且a≠1,∴ a>1.
② 当0<a<1时,有 2a-1>a2>0,此不等式无解.
综合①、②可知,实数a的取值范围是(1,+∞).……………… 12分
∴(Sn-Sn-1-1)an-1 =-an,即 anan-1-an-1 + an = 0.
∵ an≠0,若不然,则an-1 = 0,从而与a1 = 1矛盾,∴ anan-1≠0,
∴ anan-1-an-1 + an = 0两边同除以anan-1,得
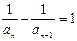 (n≥2).
(n≥2).又
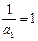 ,∴ {
,∴ {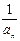 }是以1为首项,1为公差为等差数列,
}是以1为首项,1为公差为等差数列,则
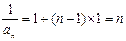 ,
,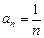 . …………………… 4分
. …………………… 4分(2)∵ bn =" an2" =
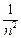 ,∴ 当 n = 1时,Tn =
,∴ 当 n = 1时,Tn = 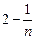 ; …… 5分
; …… 5分当n≥2时,
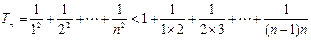
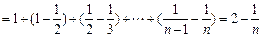 ………… 8分
………… 8分(3)
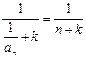 , ∴
, ∴ 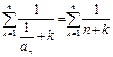 .
.设 g(n)=
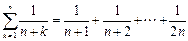 ,
,∴
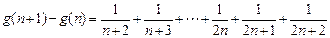
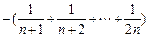
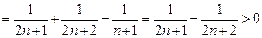 ,
,∴ g (n)为增函数,
从而 g (n)|min = g(1)=
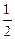 . …………………… 10分
. …………………… 10分因为 g (n)
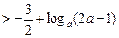 对任意正整数n都成立,
对任意正整数n都成立,所以
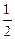
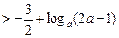 ,得 log a(2a-1)<2,即 log a(2a-1)< log a a2.
,得 log a(2a-1)<2,即 log a(2a-1)< log a a2.① 当a>1时,有 0<2a-1<a2,解得 a>
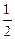 且a≠1,∴ a>1.
且a≠1,∴ a>1.② 当0<a<1时,有 2a-1>a2>0,此不等式无解.
综合①、②可知,实数a的取值范围是(1,+∞).……………… 12分

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
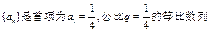 ,设
,设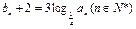 ,数列
,数列 。
。
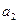 ,
,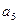 是方程
是方程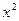
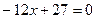 的两根, 数列
的两根, 数列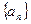 是公差为正的等差数列,数列
是公差为正的等差数列,数列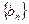 的前
的前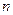 项和为
项和为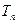 ,且
,且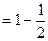
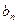
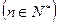 .
.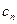 =
=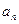
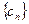 的前
的前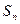 .
.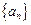 满足:
满足: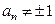 ,
,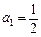 ,
,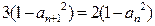 ,记数列
,记数列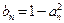 ,
,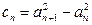 (
(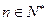 ).
).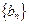 是等比数列;
是等比数列;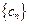 的通项公式;
的通项公式;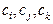 (
(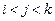 )使之成为等差数列?若存在请求出这样的不同项
)使之成为等差数列?若存在请求出这样的不同项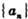 的前n项和为
的前n项和为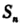 ,公差d>0,且
,公差d>0,且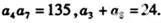
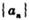 的通项公式;
的通项公式;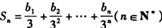 求数列
求数列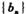 的前n项和Tn.
的前n项和Tn.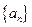 是等差数列, 若
是等差数列, 若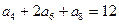 , 则该数列前11项的和为 .
, 则该数列前11项的和为 .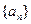 的前n项和为
的前n项和为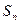 ,若
,若 ,
, ,则
,则
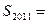
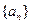 是等差数列,
是等差数列,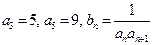 ,则数列
,则数列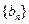 的前
的前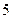 项和等于▲
项和等于▲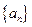 的前n项和是
的前n项和是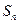 ,若
,若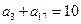 ,则
,则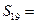 ( )
( )
