题目内容
已知函数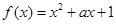 是偶函数,则函数
是偶函数,则函数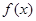 的最小值为 .
的最小值为 .
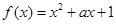 是偶函数,则函数
是偶函数,则函数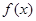 的最小值为 .
的最小值为 .1.
试题分析:因为f(x)为偶函数,所以f(-x)=f(x)恒成立,所以a=0.所以
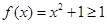 ,
,所以f(x)的最小值为1.
点评:因为此函数是偶函数,所以f(-x)=f(x)恒成立,据此可求出参数的值,也可从定义域内取两个相反数,然后根据其函数值相等建立关于a的方程求解也可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
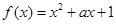 是偶函数,则函数
是偶函数,则函数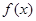 的最小值为 .
的最小值为 .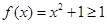 ,
,
 名校课堂系列答案
名校课堂系列答案