题目内容
【题目】如图,在三棱锥![]() 中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为
中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为![]() ,
,![]() ,二面角A-BD-C的大小为
,二面角A-BD-C的大小为![]() ,
,
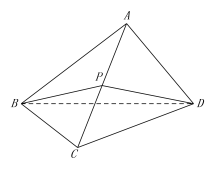
证明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)由题意可知Rt△BAD≌Rt△BCD,∴AD=CD,又P是AC的中点,∴PB⊥AC,PD⊥AC,可得AC⊥平面BDP ,结合面面垂直的判定定理即可得证。
(Ⅱ)作AM⊥ BD,M为垂足,连接PM,CM.可得AC⊥PM,AC⊥BD,所以BD⊥CM,则∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() . 可求出
. 可求出![]() 与
与![]() 的关系,即可得证。
的关系,即可得证。
(Ⅰ)证明:∵△ABC是等边三角形,AB⊥AD,CB⊥CD,
∴Rt△BAD≌Rt△BCD,∴AD=CD.
∵点P是AC的中点,∴PB⊥AC,PD⊥AC,
又![]() =P,
=P,![]() 平面BDP,
平面BDP,![]() 平面BDP,
平面BDP,
∴AC⊥平面BDP,
∵![]() 平面ACD,∴平面ACD⊥平面BDP.
平面ACD,∴平面ACD⊥平面BDP.
(Ⅱ)证明:作AM⊥ BD,M为垂足,连接PM,CM.
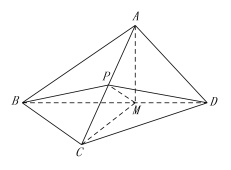
由(1)知AC⊥平面BDP,则AC⊥PM,AC⊥BD,
∵![]() ,∴BD⊥平面ACM,
,∴BD⊥平面ACM,
∴BD⊥CM,则∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() .
.
又P为AC的中点,PM⊥AC,则∠AMP=![]() ,
,
所以 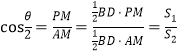 ,
,
所以![]() .
.

练习册系列答案
相关题目