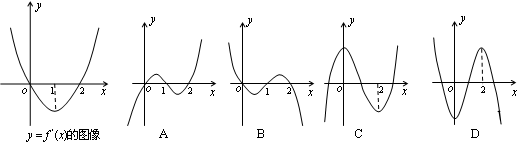
题目内容
曲线 :
: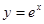 在点
在点 处的切线
处的切线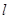 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线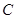 、直线
、直线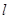 、
、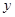 轴围成的图形面积为( )
轴围成的图形面积为( )
A.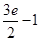 | B.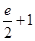 | C.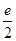 | D.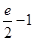 |
D
解析题分析:设点 的坐标为
的坐标为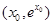 ,
,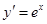 ,所以点
,所以点 处的切线的斜率为
处的切线的斜率为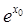 ,因为切线恰好经过坐标原点,所以
,因为切线恰好经过坐标原点,所以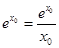 ,解得
,解得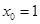 ,所以直线
,所以直线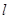 的方程为
的方程为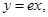 所以曲线
所以曲线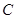 、直线
、直线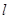 、
、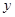 轴围成的图形面积为
轴围成的图形面积为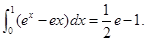
考点:本小题主要考查导数的几何意义和利用定积分求曲边图形的面积,考查学生运用数学知识解决问题的能力和数形结合思想的应用.
点评:用定积分求曲边图形的面积时,一定要写清楚积分限,而且一定要注意是上边的图形减下边的图形,所以一定要数形结合来解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线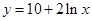 在点
在点 处的切线方程是
处的切线方程是
A. | B. |
C. | D.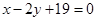 |
设定义在R上的函数 是最小正周期为
是最小正周期为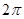 的偶函数,
的偶函数,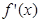 是
是 的导函数,当
的导函数,当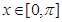 时,
时,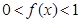 ;当
;当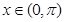 且
且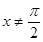 时,
时,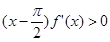 ,则函数
,则函数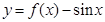 在
在 上的零点个数为
上的零点个数为
| A.2 | B.4 | C.5 | D.8 |
 等于
等于
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |
函数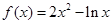 在其定义域的一个子区间
在其定义域的一个子区间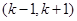 内部是单调函数,则实数
内部是单调函数,则实数 的取值范围是 ( )
的取值范围是 ( )
A.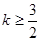 | B.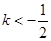 |
C.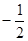 < <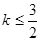 | D.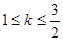 |
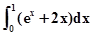 等于( )
等于( )
| A.1 | B.e-1 | C.e+1 | D.e |
若函数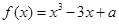 有3个不同的零点,则实数
有3个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A.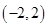 | B.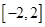 | C.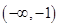 | D. |
 是定义在R上的函数,其中
是定义在R上的函数,其中 的导函数为
的导函数为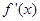 ,满足
,满足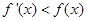 对于
对于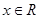 恒成立,则( )
恒成立,则( )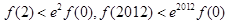
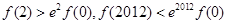
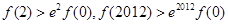
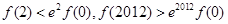
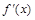 是函数
是函数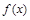 的导函数,
的导函数,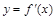 的图象如图所示,则
的图象如图所示,则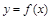 的图象最有可能的是( ).
的图象最有可能的是( ).