题目内容
曲线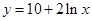 在点
在点 处的切线方程是
处的切线方程是
A. | B. |
C. | D.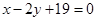 |
B
解析试题分析:根据题意研究的是曲线在某点出的切线方程,因此可知切点为(1,10),那么函数f(x)= 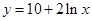 的导数为f’(x)=
的导数为f’(x)=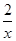 ,那么可知在x=1处的导数值为2,即为切线的斜率,因此利用点斜式方程得到为y-10=2(x-1),变形得到为
,那么可知在x=1处的导数值为2,即为切线的斜率,因此利用点斜式方程得到为y-10=2(x-1),变形得到为 ,故选B.
,故选B.
考点:本试题考查了导数的几何意义的运用。
点评:利用导数求解曲线的切线方程要注意两点:第一就是切点是谁?第二就是切线的斜率,也就是切点的导数值,然后利用点斜式方程得到结论。属于基础题。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知 为
为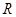 上的可导函数,且
上的可导函数,且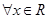 ,均有
,均有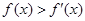 ,则有( )
,则有( )
A. , ,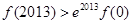 |
B. , ,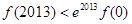 |
C. , ,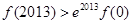 |
D. , ,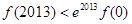 |
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当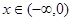 时,不等式
时,不等式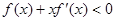 成立,若
成立,若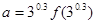 ,
,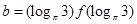 ,
,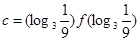 ,则
,则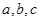 的大小关系是( )
的大小关系是( )
A.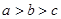 | B.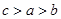 | C. | D. |
设函数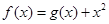 ,曲线
,曲线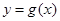 在点
在点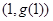 处的切线方程为
处的切线方程为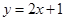 ,则曲线
,则曲线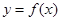 在点
在点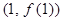 处切线的斜率为 ( )
处切线的斜率为 ( )
A.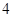 | B.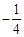 | C.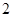 | D.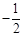 |
下列各命题中,不正确的是( )
A.若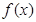 是连续的奇函数,则 是连续的奇函数,则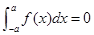 |
B.若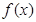 是连续的偶函数,则 是连续的偶函数,则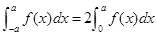 |
C.若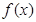 在 在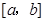 上连续且恒正,则 上连续且恒正,则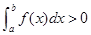 |
D.若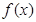 在 在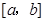 上连续,且 上连续,且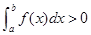 ,则 ,则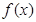 在 在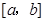 上恒正 上恒正 |
设函数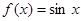 的导函数为
的导函数为 ,则
,则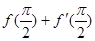 等于( )
等于( )
| A.2 | B.1 | C.0 | D.-1 |
已知 ,则函数
,则函数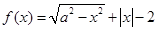 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
曲线 :
: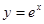 在点
在点 处的切线
处的切线 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线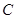 、直线
、直线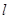 、
、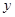 轴围成的图形面积为( )
轴围成的图形面积为( )
A.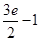 | B.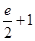 | C.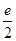 | D.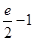 |
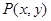 是曲线
是曲线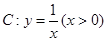 上的动点,曲线
上的动点,曲线 在点
在点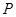 处的切线与
处的切线与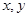 轴分别交于
轴分别交于 两点,点
两点,点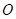 是坐标原点.给出三个结论:①
是坐标原点.给出三个结论:①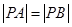 ;②△
;②△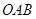 的周长有最小值
的周长有最小值 ;③曲线
;③曲线 ,使得△
,使得△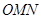 为等腰直角三角形.其中正确结论的个数是
为等腰直角三角形.其中正确结论的个数是