题目内容
设定义在R上的函数 是最小正周期为
是最小正周期为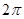 的偶函数,
的偶函数,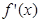 是
是 的导函数,当
的导函数,当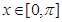 时,
时,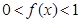 ;当
;当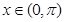 且
且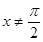 时,
时,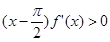 ,则函数
,则函数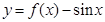 在
在 上的零点个数为
上的零点个数为
| A.2 | B.4 | C.5 | D.8 |
B
解析试题分析:由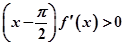 得
得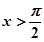 时函数递增,
时函数递增, 时函数递减;函数
时函数递减;函数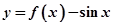 的零点个数可看作
的零点个数可看作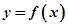 与
与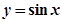 的交点个数,结合
的交点个数,结合 是最小正周期为
是最小正周期为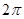 的偶函数作出它的图像与
的偶函数作出它的图像与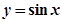 图像,由图像观察可知两函数图像有4个交点,即
图像,由图像观察可知两函数图像有4个交点,即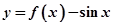 在
在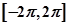 上有4个零点
上有4个零点
考点:函数零点及周期性奇偶性图像
点评:本题利用数形结合法求解函数零点省去了大量的计算

练习册系列答案
相关题目
已知函数 是定义在
是定义在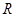 上的奇函数,且当
上的奇函数,且当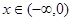 时,不等式
时,不等式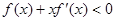 成立,若
成立,若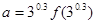 ,
,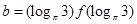 ,
,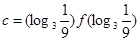 ,则
,则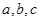 的大小关系是( )
的大小关系是( )
A.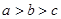 | B.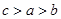 | C. | D.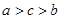 |
已知 ,则函数
,则函数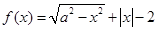 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
若函数 的导函数
的导函数 ,则函数
,则函数 的单调递减区间是( )
的单调递减区间是( )
A.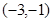 | B.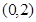 | C. | D.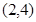 |
曲线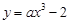 在点
在点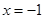 处切线的倾斜角为
处切线的倾斜角为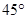 ,那么
,那么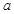 的值为( )
的值为( )
A.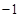 | B. | C.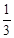 | D. |
已知定义在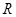 上的函数
上的函数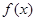 满足
满足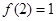 ,且
,且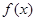 的导函数
的导函数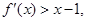 则不等式
则不等式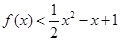 的解集为( )
的解集为( )
A.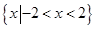 | B.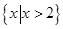 | C.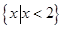 | D.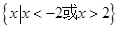 |
曲线 :
: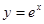 在点
在点 处的切线
处的切线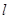 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线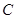 、直线
、直线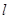 、
、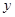 轴围成的图形面积为( )
轴围成的图形面积为( )
A.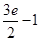 | B.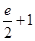 | C.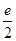 | D.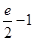 |
设函数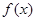 在R上可导,其导函数为
在R上可导,其导函数为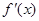 ,且函数
,且函数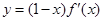 的图像如图所示,则下列结论中一定成立的是( )
的图像如图所示,则下列结论中一定成立的是( )
A.函数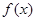 有极大值 有极大值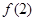 和极小值 和极小值 |
B.函数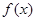 有极大值 有极大值 和极小值 和极小值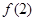 |
C.函数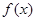 有极大值 有极大值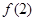 和极小值 和极小值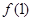 |
D.函数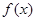 有极大值 有极大值 和极小值 和极小值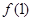 |
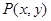 是曲线
是曲线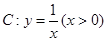 上的动点,曲线
上的动点,曲线 在点
在点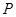 处的切线与
处的切线与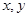 轴分别交于
轴分别交于 两点,点
两点,点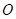 是坐标原点.给出三个结论:①
是坐标原点.给出三个结论:①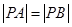 ;②△
;②△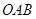 的周长有最小值
的周长有最小值 ;③曲线
;③曲线 ,使得△
,使得△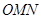 为等腰直角三角形.其中正确结论的个数是
为等腰直角三角形.其中正确结论的个数是