Question

【题目】函数f（x）=ln（x+1）﹣ （a＞1）．
（1）讨论f（x）的单调性；
（2）设a1=1，an+1=ln（an+1），证明： ＜an≤ ．

Answer 1

【答案】
（1）解：函数f（x）的定义域为（﹣1，+∞），f′（x）= ，

①当1＜a＜2时，若x∈（﹣1，a2﹣2a），则f′（x）＞0，此时函数f（x）在（﹣1，a2﹣2a）上是增函数，

若x∈（a2﹣2a，0），则f′（x）＜0，此时函数f（x）在（a2﹣2a，0）上是减函数，

若x∈（0，+∞），则f′（x）＞0，此时函数f（x）在（0，+∞）上是增函数．

②当a=2时，f′（x）≥0，此时函数f（x）在（﹣1，+∞）上是增函数，

③当a＞2时，若x∈（﹣1，0），则f′（x）＞0，此时函数f（x）在（﹣1，0）上是增函数，

若x∈（0，a2﹣2a），则f′（x）＜0，此时函数f（x）在（0，a2﹣2a）上是减函数，

若x∈（a2﹣2a，+∞），则f′（x）＞0，此时函数f（x）在（a2﹣2a，+∞）上是增函数．

（2）解：由（1）知，当a=2时，此时函数f（x）在（﹣1，+∞）上是增函数，

当x∈（0，+∞）时，f（x）＞f（0）=0，

即ln（x+1）＞ ，（x＞0），

又由（1）知，当a=3时，f（x）在（0，3）上是减函数，

当x∈（0，3）时，f（x）＜f（0）=0，ln（x+1）＜ ，

下面用数学归纳法进行证明 ＜an≤ 成立，

①当n=1时，由已知

，故结论成立．

②假设当n=k时结论成立，即 ，

则当n=k+1时，an+1=ln（an+1）＞ln（ +1） ，

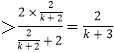an+1=ln（an+1）＜ln（ +1） ，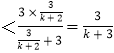

即当n=k+1时， 成立，

综上由①②可知，对任何n∈N结论都成立．

【解析】（1）求函数的导数，通过讨论a的取值范围，即可得到f（x）的单调性；（2）利用数学归纳法即可证明不等式．
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减)，还要掌握数学归纳法的定义(数学归纳法是证明关于正整数n的命题的一种方法)的相关知识才是答题的关键．