题目内容
已知函数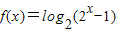 ,
,(1)求f(x)的定义域;
(2)判断函数f(x)的单调性,并用定义证明.
【答案】分析:(1)根据使函数的解析式有意义的原则,结合对数函数的真数部分必须大于0,可以构造关于x的不等式,可得函数的定义域;
(2)取x1,x2∈(0,+∞)且x1<x2,根据对数的运算性质及指数函数的性质,判断出f(x1),f(x2)的大小,结合函数单调性的定义可得函数的单调性.
解答:解:(1)要使函数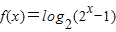 的解析式有意义
的解析式有意义
自变量必须满足2x-1>0
即2x>1=2
∴x>0,
即f(x)的定义域为{x|x>0}---------(5分)
(2)f(x)的在定义域内为增函数.理由如下:
设x1,x2∈(0,+∞)且x1<x2,
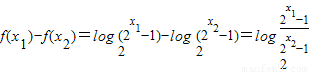 -----------------(8分)
-----------------(8分)
∵x2>x1>0
∴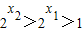
∴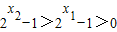
∴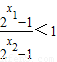 ------------------------------------(10分)
------------------------------------(10分)
f(x1)-f(x2)<0,
即f(x1)<f(x2),
即函数f(x)为定义域内增函数--------------------(12分)
点评:本题考查的知识点是对数函数的图象和性质,函数的定义域及函数的单调性,其中熟练掌握函数定义域的求法及函数单调性的证明方法是解答的关键.
(2)取x1,x2∈(0,+∞)且x1<x2,根据对数的运算性质及指数函数的性质,判断出f(x1),f(x2)的大小,结合函数单调性的定义可得函数的单调性.
解答:解:(1)要使函数
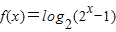 的解析式有意义
的解析式有意义自变量必须满足2x-1>0
即2x>1=2
∴x>0,
即f(x)的定义域为{x|x>0}---------(5分)
(2)f(x)的在定义域内为增函数.理由如下:
设x1,x2∈(0,+∞)且x1<x2,
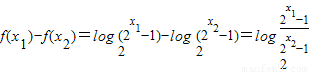 -----------------(8分)
-----------------(8分)∵x2>x1>0
∴
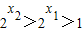
∴
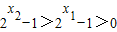
∴
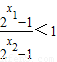 ------------------------------------(10分)
------------------------------------(10分)f(x1)-f(x2)<0,
即f(x1)<f(x2),
即函数f(x)为定义域内增函数--------------------(12分)
点评:本题考查的知识点是对数函数的图象和性质,函数的定义域及函数的单调性,其中熟练掌握函数定义域的求法及函数单调性的证明方法是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.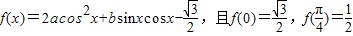 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.