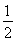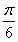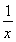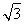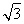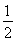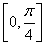题目内容
设函数f(x)=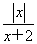 -ax2,a∈R.
-ax2,a∈R.
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有四个不同的零点,求a的取值范围.
(1)0,x=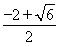 ,x=
,x=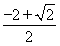 ,x=
,x=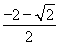 (2)见解析(3)(1,+∞)
(2)见解析(3)(1,+∞)
【解析】(1)【解析】
当x≥0时,由f(x)=0,得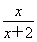 -2x2=0,即x(2x2+4x-1)=0,解得x=0或x=
-2x2=0,即x(2x2+4x-1)=0,解得x=0或x=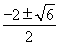 (舍负);
(舍负);
当x<0时,由f(x)=0,得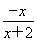 -2x2=0,
-2x2=0,
即x(2x2+4x+1)=0(x≠-2),解得x=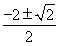 .
.
综上所述,函数f(x)的零点为0,x=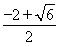 ,x=
,x=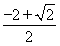 ,x=
,x=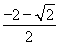 .
.
(2)证明:当a>0且x>0时,由f(x)=0,得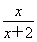 -ax2=0,即ax2+2ax-1=0.
-ax2=0,即ax2+2ax-1=0.
记g(x)=ax2+2ax-1,则函数g(x)的图象是开口向上的抛物线.
又g(0)=-1<0,所以函数g(x)在(0,+∞)内有且仅有一个零点,
即函数f(x)在区间(0,+∞)内有且仅有一个零点.
(3)【解析】
易知0是函数f(x)的零点.
对于x>0,由(2)知,当a>0时,函数f(x)在区间(0,+∞)内有且仅有一个零点;
当a≤0时,g(x)=ax2+2ax-1<0恒成立,因此函数f(x)在区间(0,+∞)内无零点.
于是,要使函数f(x)有四个不同的零点,函数f(x)在区间(-∞,0)内就要有两个不同的零点.
当x<0时,由f(x)=0,得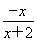 -ax2=0,即ax2+2ax+1=0(x≠-2).①
-ax2=0,即ax2+2ax+1=0(x≠-2).①
因为a=0不符合题意,所以①式可化为x2+2x+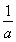 =0(x≠-2),即x2+2x=-
=0(x≠-2),即x2+2x=-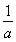 =0.
=0.
作出函数h(x)=x2+2x(x<0)的图象便知-1<-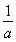 <0,得a>1,
<0,得a>1,
综上所述,a的取值范围是(1,+∞).

练习册系列答案
相关题目