题目内容
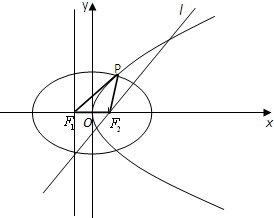 设抛物线C1 :y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=
设抛物线C1 :y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=| 1 | 2 |
(1)当m=1时,直线l经过椭圆C2的右焦点F2,与抛物线C1交于A1、A2,如果弦长|A1A2|等于三角形PF1F2的周长,求直线l的斜率.
(2)求最小实数m,使得三角形PF1F2的边长是自然数.
分析:(1)m=1时,F2(1,0),由此能求出椭圆方程3x2+4y2=12.设l:y=k(x-1),联立
得k2x2-(2k2+4)x+k2=0,由此利用弦长公式能求出直线的斜率.
(2)设椭圆长半轴为a,半焦距为c,由题设有c=m,a=2m,|F1F2|=2m.设|PF1|=r1,|PF2|=r2,有r1+r2=2a=4m,设P(x0,y0),对于抛物线C1,r2=x0+m.由此能推导出使得三角形PF1F2的边长是连续的自然数的最小实数.
|
(2)设椭圆长半轴为a,半焦距为c,由题设有c=m,a=2m,|F1F2|=2m.设|PF1|=r1,|PF2|=r2,有r1+r2=2a=4m,设P(x0,y0),对于抛物线C1,r2=x0+m.由此能推导出使得三角形PF1F2的边长是连续的自然数的最小实数.
解答:解:(1)∵抛物线C1 :y2=4mx(m>0),
∴m=1时,F2(1,0),
∵c=1 e=
∴ a=2 , b2=a2-c2=3,
故椭圆方程为
+
=1,即3x2+4y2=12.
依题意知直线l存在斜率,设l:y=k(x-1)
联立
得k2x2-(2k2+4)x+k2=0.…3分
∵直线l与抛物线C1有两个交点,∴k≠0,
设A1(x1,y1),A2(x2,y2),弦A1A2的中点M(x,y),
由韦达定理得x1+x2=
=2+
,x1x2=1…..5分
则 |A1A2|=
|x1-x2|=
=
=
=4
=4•
…8分
三角形PF1F2的周长=2a+2c=6,
由
=6,解得 k=±
.
故直线l的斜率为±
.…9分
(2)设椭圆长半轴为a,半焦距为c,由题设有c=m,a=2m,|F1F2|=2m.
又设|PF1|=r1,|PF2|=r2,有r1+r2=2a=4m
设P(x0,y0),对于抛物线C1,r2=x0+m;
对于椭圆C2,
=e=
,
即r2=
(4m-x0)…..12分
由x0+m=
(4m-x0),解得 x0=
m,
∴r2=
m,从而 r1=
m.
因此,三角形PF1F2的边长分别是
m ,
m ,
m.…13分
使得三角形PF1F2的边长是连续的自然数的最小实数m=3.…14分
∴m=1时,F2(1,0),
∵c=1 e=
| 1 |
| 2 |
故椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
依题意知直线l存在斜率,设l:y=k(x-1)
联立
|
∵直线l与抛物线C1有两个交点,∴k≠0,
设A1(x1,y1),A2(x2,y2),弦A1A2的中点M(x,y),
由韦达定理得x1+x2=
| 2k2+4 |
| k2 |
| 4 |
| k2 |
则 |A1A2|=
| 1+k2 |
| (1+k2)[(x1+x2)2-4x1x2] |
=
(1+k2)[(2+
|
(1+k2)(
|
=4
(1+k2)
|
| 1+k2 |
| k2 |
三角形PF1F2的周长=2a+2c=6,
由
| 4(1+k2) |
| k2 |
| 2 |
故直线l的斜率为±
| 2 |
(2)设椭圆长半轴为a,半焦距为c,由题设有c=m,a=2m,|F1F2|=2m.
又设|PF1|=r1,|PF2|=r2,有r1+r2=2a=4m
设P(x0,y0),对于抛物线C1,r2=x0+m;
对于椭圆C2,
| r2 | ||
|
| 1 |
| 2 |
即r2=
| 1 |
| 2 |
由x0+m=
| 1 |
| 2 |
| 2 |
| 3 |
∴r2=
| 5 |
| 3 |
| 7 |
| 3 |
因此,三角形PF1F2的边长分别是
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
使得三角形PF1F2的边长是连续的自然数的最小实数m=3.…14分
点评:本题考查直线斜率的求法,考查使得三角形周长是连续的自然数的最小实数的求法.解题时要认真审题,注意椭圆、抛物线、直线与圆锥曲线的位置关系的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e= 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=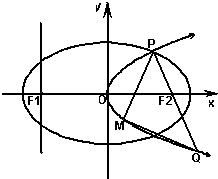 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=