题目内容
设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2,以F1,F2为焦点,离心率为| 1 | 2 |
(1)若椭圆的长半轴长为2,求抛物线方程;
(2)在(1)的条件下,直线l经过椭圆C2的右焦点F2,与抛物线C1交于A1,A2两点,如果|A1A2|等于△PF1F2的周长,求l的斜率;
(3)是否存在实数m,使得△PF1F2的边长是连续的自然数?若存在,求出m的值,若不存在,说明理由.
分析:(1)由椭圆C2的离心率为
,长半轴长为2,即可求出a,b,c的值,进而求出抛物线交点坐标,抛物线方程也就能求出.
(2)在(1)的条件下,可求出椭圆方程,这样,焦点三角形△PF1F2的周长可知,也即|A1A2|.再利用弦长公式即可.
(3)先假设存在实数m,使得△PF1F2的边长是连续的自然数,因为中间线段长度为2m,所以,最短线段长度为2m-1,再用抛物线定义即可求出.
| 1 |
| 2 |
(2)在(1)的条件下,可求出椭圆方程,这样,焦点三角形△PF1F2的周长可知,也即|A1A2|.再利用弦长公式即可.
(3)先假设存在实数m,使得△PF1F2的边长是连续的自然数,因为中间线段长度为2m,所以,最短线段长度为2m-1,再用抛物线定义即可求出.
解答:解:(1)∵椭圆C2的离心率为
,长半轴长为2,∴
,
∵物线C1:y2=4mx(m>0)的焦点为椭圆右焦点,∴
=1,∴抛物线方程y2=4x
(2)由(1)可知,椭圆方程为
+
= 1,所以△PF1F2的周长为2a+2c=6.
①当直线l斜率存在时,设直线方程为y=k(x-1),代入y2=4x,得k2x2-(2k2+4)x+k2=0,
∴x1+x2=2+
,x1x2=1,
∴|A1A2|=
|x1-x2|=
+
-5=0,解得,k=±
.
②当直线l斜率不存在时,A1点坐标为(1,
)A2(1,-
),∴|A1A2|=2
≠6,不成立.
综上,直线l的斜率为±
.
(3)由题意可知,椭圆中c=m.椭圆C2离心率为
,∴a=2c.
∴椭圆方程为
+
= 1由,
得P点横坐标为
m,在椭圆中,|PF1|+|PF2|=2a=4m,
|F1F2|=2m,∴|PF2|,|F1F2|,|PF1|成等差数列,
假设存在实数m,使得△PF1F2的边长是连续的自然数,则PF2|=|F1F2|-1=2m-1,又因为P在抛物线上,
∴|F1F2|=
m+m,∴m=3
| 1 |
| 2 |
| 3 |
∵物线C1:y2=4mx(m>0)的焦点为椭圆右焦点,∴
| p |
| 2 |
(2)由(1)可知,椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
①当直线l斜率存在时,设直线方程为y=k(x-1),代入y2=4x,得k2x2-(2k2+4)x+k2=0,
∴x1+x2=2+
| 4 |
| k2 |
∴|A1A2|=
| 1+k2 |
| 4 |
| k4 |
| 8 |
| k2 |
| 2 |
②当直线l斜率不存在时,A1点坐标为(1,
| ||
| 2 |
| ||
| 2 |
| 3 |
综上,直线l的斜率为±
| 2 |
(3)由题意可知,椭圆中c=m.椭圆C2离心率为
| 1 |
| 2 |
∴椭圆方程为
| x2 |
| 4m2 |
| y2 |
| 3m2 |
|
| 2 |
| 3 |
|F1F2|=2m,∴|PF2|,|F1F2|,|PF1|成等差数列,
假设存在实数m,使得△PF1F2的边长是连续的自然数,则PF2|=|F1F2|-1=2m-1,又因为P在抛物线上,
∴|F1F2|=
| 2 |
| 3 |
点评:本题考查了椭圆,抛物线,与直线的位置关系,综合性强,做题时认真观察,找出切入点.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e= 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率e=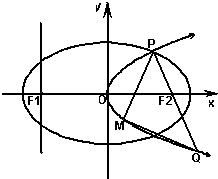 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=