题目内容
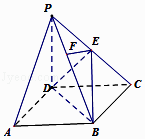
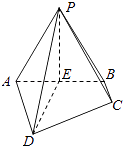
【题目】如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= ![]() AD.
AD. 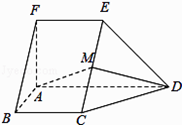
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(3)求锐二面角A﹣CD﹣E的余弦值.
【答案】
(1)解:如图所示,建立空间直角坐标系,点A为坐标原点.

设AB=1,依题意得B(1,0,0),C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),M( ![]() ,1,
,1, ![]() ).
).
![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,﹣1,1),
=(0,﹣1,1),
于是cos< ![]() ,
, ![]() >=
>= 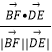 =
= ![]() =
= ![]() .
.
所以异面直线BF与DE所成的角的大小为60°
(2)证明:由 ![]() =(
=( ![]() ,1,
,1, ![]() ),
), ![]() =(﹣1,0,1),
=(﹣1,0,1),
![]() =(0,2,0),可得
=(0,2,0),可得 ![]()
![]() =0,
=0, ![]()
![]() =0.
=0.
因此,CE⊥AM,CE⊥AD.
又AM∩AD=A,故CE⊥平面AMD.
而CE∥平面CDE,所以平面AMD⊥平面CDE
(3)解:设平面CDE的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 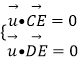 于是
于是 ![]() 令x=1,可得
令x=1,可得 ![]() =(1,1,1).
=(1,1,1).
又由题设,平面ACD的一个法向量为v=(0,0,1).
所以, ![]() =
= ![]() =
= ![]() =
= ![]() .
.
因为二面角A﹣CD﹣E为锐角,所以其余弦值为 ![]()
【解析】(1)建立空间直角坐标系,点A为坐标原点.设AB=1,求出B,C,D,E,F,M.求出 ![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,﹣1,1),利用空间向量的数量积求解异面直线BF与DE所成的角的大小.(2)证明
=(0,﹣1,1),利用空间向量的数量积求解异面直线BF与DE所成的角的大小.(2)证明 ![]()
![]() =0,
=0, ![]()
![]() =0.推出CE⊥平面AMD.然后证明平面AMD⊥平面CDE.(3)求出平面CDE的法向量为
=0.推出CE⊥平面AMD.然后证明平面AMD⊥平面CDE.(3)求出平面CDE的法向量为 ![]() ,平面ACD的一个法向量为v,利用空间向量的数量积求解二面角的余弦值.
,平面ACD的一个法向量为v,利用空间向量的数量积求解二面角的余弦值.
【考点精析】掌握异面直线及其所成的角和平面与平面垂直的判定是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案