题目内容
已知函数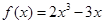 .
.
(1)求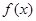 在区间
在区间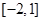 上的最大值;
上的最大值;
(2)若过点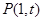 存在3条直线与曲线
存在3条直线与曲线 相切,求t的取值范围;
相切,求t的取值范围;
(3)问过点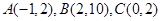 分别存在几条直线与曲线
分别存在几条直线与曲线 相切?(只需写出结论)
相切?(只需写出结论)
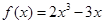 .
.(1)求
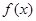 在区间
在区间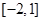 上的最大值;
上的最大值;(2)若过点
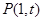 存在3条直线与曲线
存在3条直线与曲线 相切,求t的取值范围;
相切,求t的取值范围;(3)问过点
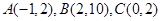 分别存在几条直线与曲线
分别存在几条直线与曲线 相切?(只需写出结论)
相切?(只需写出结论)试题分析:(1)求导数,导数等于0求出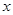 ,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.
,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.
(1)由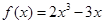 得
得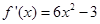 ,令
,令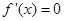 ,得
,得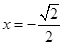 或
或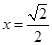 ,
,
因为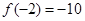 ,
,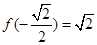 ,
,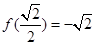 ,
,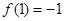 ,
,
所以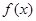 在区间
在区间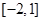 上的最大值为
上的最大值为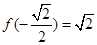 .
.
(2)设过点P(1,t)的直线与曲线 相切于点
相切于点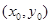 ,则
,则
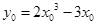 ,且切线斜率为
,且切线斜率为 ,所以切线方程为
,所以切线方程为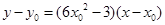 ,
,
因此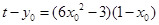 ,整理得:
,整理得: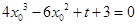 ,
,
设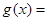
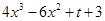 ,则“过点
,则“过点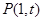 存在3条直线与曲线
存在3条直线与曲线 相切”等价于“
相切”等价于“ 有3个不同零点”,
有3个不同零点”, 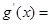
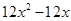 =
=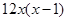 ,
,
 与
与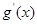 的情况如下:
的情况如下:
所以,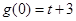 是
是 的极大值,
的极大值,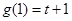 是
是 的极小值,
的极小值,
当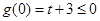 ,即
,即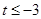 时,此时
时,此时 在区间
在区间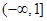 和
和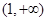 上分别至多有1个零点,所以
上分别至多有1个零点,所以
 至多有2个零点,
至多有2个零点,
当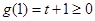 ,
,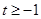 时,此时
时,此时 在区间
在区间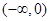 和
和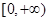 上分别至多有1个零点,所以
上分别至多有1个零点,所以
 至多有2个零点.
至多有2个零点.
当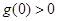 且
且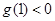 ,即
,即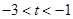 时,因为
时,因为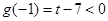 ,
,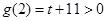 ,
,
所以 分别为区间
分别为区间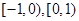 和
和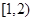 上恰有1个零点,由于
上恰有1个零点,由于 在区间
在区间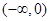 和
和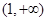 上单调,所以
上单调,所以 分别在区间
分别在区间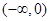 和
和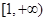 上恰有1个零点.
上恰有1个零点.
综上可知,当过点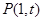 存在3条直线与曲线
存在3条直线与曲线 相切时,t的取值范围是
相切时,t的取值范围是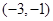 .
.
(3)过点A(-1,2)存在3条直线与曲线 相切;
相切;
过点B(2,10)存在2条直线与曲线 相切;
相切;
过点C(0,2)存在1条直线与曲线 相切.
相切.
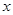 ,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.
,再代入原函数解析式,最后比较大小,即可;(2)设切点,由相切得出切线方程,然后列表并讨论求出结果;(3)由(2)容易得出结果.(1)由
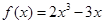 得
得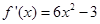 ,令
,令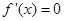 ,得
,得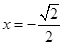 或
或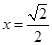 ,
,因为
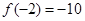 ,
,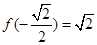 ,
,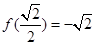 ,
,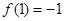 ,
,所以
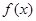 在区间
在区间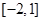 上的最大值为
上的最大值为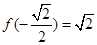 .
.(2)设过点P(1,t)的直线与曲线
 相切于点
相切于点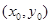 ,则
,则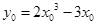 ,且切线斜率为
,且切线斜率为 ,所以切线方程为
,所以切线方程为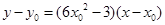 ,
,因此
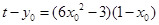 ,整理得:
,整理得: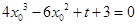 ,
,设
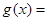
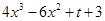 ,则“过点
,则“过点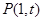 存在3条直线与曲线
存在3条直线与曲线 相切”等价于“
相切”等价于“ 有3个不同零点”,
有3个不同零点”, 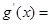
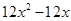 =
=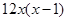 ,
, 与
与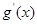 的情况如下:
的情况如下: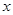 | 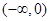 | 0 | 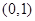 | 1 | 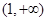 |
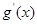 | + | 0 | 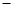 | 0 | + |
 |  | t+3 |  | 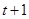 |  |
所以,
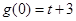 是
是 的极大值,
的极大值,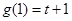 是
是 的极小值,
的极小值,当
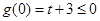 ,即
,即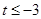 时,此时
时,此时 在区间
在区间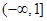 和
和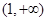 上分别至多有1个零点,所以
上分别至多有1个零点,所以 至多有2个零点,
至多有2个零点,当
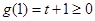 ,
,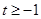 时,此时
时,此时 在区间
在区间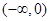 和
和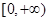 上分别至多有1个零点,所以
上分别至多有1个零点,所以 至多有2个零点.
至多有2个零点.当
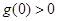 且
且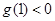 ,即
,即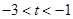 时,因为
时,因为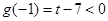 ,
,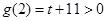 ,
,所以
 分别为区间
分别为区间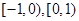 和
和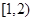 上恰有1个零点,由于
上恰有1个零点,由于 在区间
在区间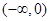 和
和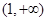 上单调,所以
上单调,所以 分别在区间
分别在区间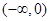 和
和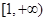 上恰有1个零点.
上恰有1个零点.综上可知,当过点
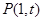 存在3条直线与曲线
存在3条直线与曲线 相切时,t的取值范围是
相切时,t的取值范围是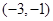 .
.(3)过点A(-1,2)存在3条直线与曲线
 相切;
相切;过点B(2,10)存在2条直线与曲线
 相切;
相切;过点C(0,2)存在1条直线与曲线
 相切.
相切.
练习册系列答案
相关题目
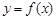 在点(x0,y0)处的切线方程为
在点(x0,y0)处的切线方程为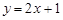 ,则
,则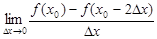 等于( )
等于( )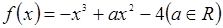 .
.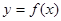 的图象在点
的图象在点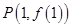 处的切线的倾斜角为
处的切线的倾斜角为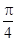 ,求
,求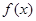 在
在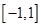 上的最小值;
上的最小值;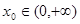 ,使
,使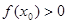 ,求a的取值范围.
,求a的取值范围.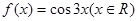 ,则曲线
,则曲线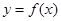 在
在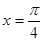 处的切线的斜率为( )
处的切线的斜率为( )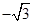
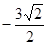
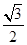
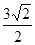
 ,
,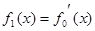 ,
,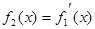 ,……,
,……,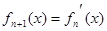 ,
,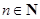 ,则
,则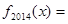 ( )
( )
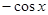
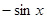
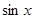
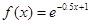 在x=4处的导数
在x=4处的导数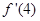 = .
= .