题目内容
设 是正数组成的数列,
是正数组成的数列, .若点
.若点 在函数
在函数 的导函数
的导函数 图像上.
图像上.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,是否存在最小的正数
,是否存在最小的正数 ,使得对任意
,使得对任意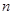
 都有
都有 成立?请说明理由.
成立?请说明理由.
(1)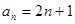 ;(2)存在最小的正数
;(2)存在最小的正数 .
.
解析试题分析:(1)由点 在函数
在函数 的导函数
的导函数 图像上可得
图像上可得 的递推公式,然后由递推公式
的递推公式,然后由递推公式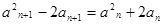 整理得
整理得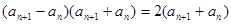 ,再由
,再由 是正数数列得
是正数数列得 ,从而知其为等差数列而得到通项公式;(2)数列
,从而知其为等差数列而得到通项公式;(2)数列 的通项公式代入,得到
的通项公式代入,得到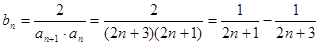 ,即可通过裂项相消法解决
,即可通过裂项相消法解决 问题.注意凡是类似于通项公式为
问题.注意凡是类似于通项公式为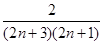 基本都可用裂项相消法予以解决.
基本都可用裂项相消法予以解决.
试题解析:(1)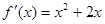 1分
1分
由点 在
在 图像上,得
图像上,得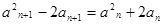 2分
2分
整理得: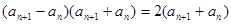 4分
4分
∵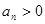 ,∴
,∴ 5分
5分
∴ 是首项为
是首项为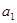 =3,公差为2的等差数列.
=3,公差为2的等差数列.
∴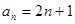 6分
6分
(2)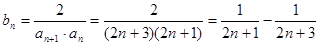 9分
9分
∴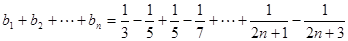 10分
10分
=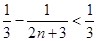 12分
12分
∴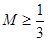 ∴存在最小的正数
∴存在最小的正数 ,使得不等式成立. 14分
,使得不等式成立. 14分
考点:1.常见函数的导数公式;2.等差数列的通项公式;3.裂项相消法.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的通项
的通项 ,
, .
.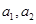 ;
;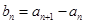 ,求数列
,求数列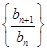 的最大项和最小项.
的最大项和最小项.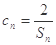 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证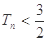
 (
( 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前 型数列。
型数列。 是首项
是首项 的
的 的值;
的值; 是
是 试求
试求 与
与 的递推关系,并证明
的递推关系,并证明 对
对 的各项均为正数,
的各项均为正数, 为其前
为其前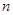 项和,对于任意的
项和,对于任意的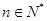 ,满足关系式
,满足关系式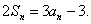
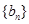 的通项公式是
的通项公式是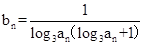 ,前
,前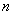 项和为
项和为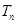 ,求证:对于任意的正整数
,求证:对于任意的正整数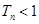 .
.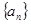 的前
的前 项和为
项和为 ,首项
,首项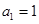 ,点
,点 在曲线
在曲线 上.
上. ;
; 的通项公式
的通项公式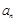 ;
; ,
, 表示数列
表示数列 的前项和,若
的前项和,若 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的前
的前 项和
项和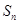 ,满足:
,满足: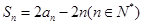 .
.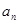 ;
;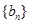 的满足
的满足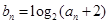 ,
,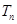 为数列
为数列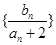 的前
的前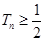 .
. 的前
的前 项和为
项和为 ,若
,若 ,
, ,
, .
.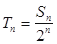 ,
, ;
; ,求
,求 的取值范围.
的取值范围.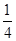 an bn,求数列{cn}的前n项和Tn.
an bn,求数列{cn}的前n项和Tn.