题目内容
【题目】已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=﹣ln(1﹣x),函数f(x)= ![]() ,若f(2﹣x2)>f(x),则x的取值范围是( )
,若f(2﹣x2)>f(x),则x的取值范围是( )
A.(﹣∞,﹣2)∪(1,+∞)
B.(﹣∞,1)∪(2,+∞)
C.(﹣2,1)
D.(1,2)
【答案】C
【解析】解:∵g(x)是定义在R上的奇函数,且当x<0时,g(x)=﹣ln(1﹣x), ∴当x>0时,﹣x<0,g(﹣x)=﹣ln(1+x),
即当x>0时,g(x)=ln(1+x),
∵函数f(x)= ![]() ,
,
∴函数f(x)= ![]() ,
,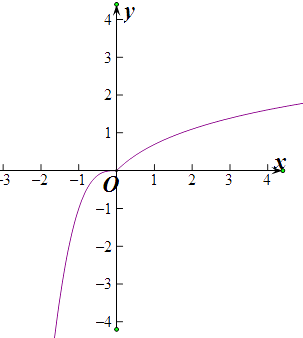
可判断f(x)= ![]() ,在(﹣∞,+∞)单调递增,
,在(﹣∞,+∞)单调递增,
∵f(2﹣x2)>f(x),
∴2﹣x2>x,
解得:﹣2<x<1,
故选:C
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目