题目内容
14.设函数f(x)=1-|x|,g(x)=-1+|x|,则函数F(x)=f[g(x)]的图象是( )| A. |  | B. | 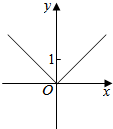 | ||
| C. |  | D. | 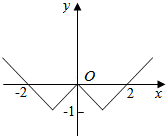 |
分析 先根据绝对值函数,去掉绝对值,得到F(x)=$\left\{\begin{array}{l}{2-x,x>1}\\{2+x,x<-1}\\{x,0≤x≤1}\\{-x,-1≤x<0}\end{array}\right.$根据每段函数的性质即可得到答案.
解答 解:∵f(x)=1-|x|,g(x)=-1+|x|,
∴F(x)=f[g(x)]=1-|-1+|x||=$\left\{\begin{array}{l}{2-|x|,|x|>1}\\{|x|,|x|≤1}\end{array}\right.$=$\left\{\begin{array}{l}{2-x,x>1}\\{2+x,x<-1}\\{x,0≤x≤1}\\{-x,-1≤x<0}\end{array}\right.$
即当x>1和-1≤x<0时,函数为增函数,
故选:C.
点评 本题考查了绝对值函数的图象问题,关键是化为分段函数,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
4.设$\frac{ai}{1-i}$=-1+i,其中i是虚数单位,那么实数a=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
9.设O为坐标原点,直线l经过点P(1,1)且与OP垂直,则直线l的方程为( )
| A. | x+y+2=0 | B. | x+y-1=0 | C. | x+y=0 | D. | x+y-2=0 |
6.已知复数z=2+i(i为虚数单位),则复数z在复平面上的对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
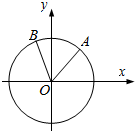 如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求
如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求