题目内容
如图,抛物线关于 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点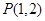 、
、 、
、 均在抛物线上.
均在抛物线上.
(1)写出该抛物线的方程及其准线方程;
(2)当 与
与 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线 的斜率.
的斜率.
(1)故所求抛物线的方程是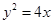 ,准线方程是
,准线方程是 ;(2)
;(2)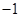 .
.
解析试题分析:(I)设出抛物线的方程,把点P代入抛物线求得p则抛物线的方程可得,进而求得抛物线的准线方程.
(2)设直线PA的斜率为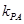 ,直线PB的斜率为
,直线PB的斜率为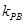 ,则可分别表示
,则可分别表示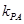 和
和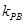 ,根据倾斜角互补可知
,根据倾斜角互补可知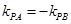 ,进而求得
,进而求得 的值,把A,B代入抛物线方程两式相减后即可求得直线AB的斜率.
的值,把A,B代入抛物线方程两式相减后即可求得直线AB的斜率.
试题解析:(I)由已知条件,可设抛物线的方程为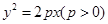
因为点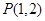 在抛物线上,所以
在抛物线上,所以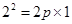 ,得
,得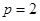 . 2分
. 2分
故所求抛物线的方程是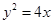 , 准线方程是
, 准线方程是 . 4分
. 4分
(2)设直线 的方程为
的方程为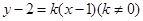 ,
,
即: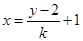 ,代入
,代入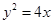 ,消去
,消去 得:
得: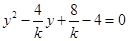 . 5分
. 5分
设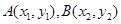 ,由韦达定理得:
,由韦达定理得: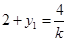 ,即:
,即: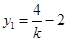 . 7分
. 7分
将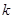 换成
换成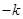 ,得
,得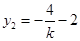 ,从而得:
,从而得: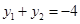 , 9分
, 9分
直线 的斜率
的斜率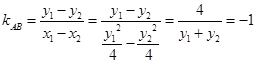 . 12分.
. 12分.
考点:抛物线的应用.

练习册系列答案
相关题目
 :
: 的准线与
的准线与 轴交于点
轴交于点 ,焦点为
,焦点为 ;椭圆
;椭圆 以
以 .设
.设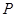 是
是
 过
过 两点,且
两点,且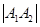 等于
等于 的周长,求
的周长,求 的离心率为
的离心率为 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切.
相切. 的标准方程;
的标准方程; 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 、
、 两点,且
两点,且 ,又点
,又点 关于原点
关于原点 的对称点为点
的对称点为点 ,试问
,试问 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过

 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围. 的短半轴长为
的短半轴长为 ,动点
,动点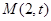
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上. 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;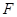 是椭圆的右焦点,过点
是椭圆的右焦点,过点 ,
, 的长为定值,并求出这个定值.
的长为定值,并求出这个定值. :
: ,命题
,命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.
轴上的双曲线. 的取值范围;
的取值范围; ”为真,命题“
”为真,命题“ ”为假,求实数
”为假,求实数 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线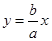 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
 的面积的最大值.
的面积的最大值.  =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,一条准线方程为x=
,一条准线方程为x=
 经过点
经过点 ,且两焦点与短轴的两个端点的连线构成一正方形.
,且两焦点与短轴的两个端点的连线构成一正方形.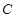 的方程;
的方程; 与椭圆
与椭圆 交于
交于 ,
, 两点,若线段
两点,若线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求
 为原点)面积的最大值.
为原点)面积的最大值.