题目内容
函数f(x)=[x]的函数值表示不超过x的最大整数,如[1.6]=1,[2]=2,已知0≤x<4.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)记函数g(x)=x-f(x),在给出的坐标系中作出函数g(x)的图象;
(Ⅲ)若方程g(x)-loga(x- )=0(a>0且a≠1)有且仅有一个实根,求a的取值范围.
)=0(a>0且a≠1)有且仅有一个实根,求a的取值范围.
解:(Ⅰ)由题意,
①当0≤x<1时,f(x)=[x]=0;②当1≤x<2时,f(x)=[x]=1;
③当2≤x<3时,f(x)=[x]=2;④当3≤x<4时,f(x)=[x]=3;
所以f(x)=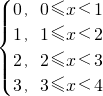 .
.
(Ⅱ) g(x)=x-f(x)=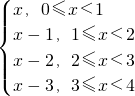 ,图象如图所示:
,图象如图所示:
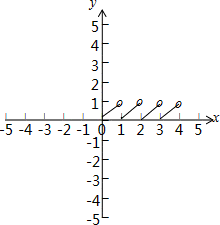
(Ⅲ)方程g(x)-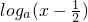 =0仅有一根等价于g(x)与h(x)=
=0仅有一根等价于g(x)与h(x)=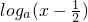 图象仅有一个交点,
图象仅有一个交点,
由图象可知0<a<1 时,h(1)=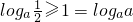 ,解得
,解得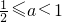 ;
;
a>1时,h(2)=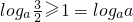 或
或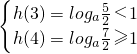 ,解得1<a≤
,解得1<a≤ 或
或 .
.
综上,a的范围是[ ,1)∪(1,
,1)∪(1, ]∪(
]∪( ,
, ].
].
分析:(Ⅰ)按照f(x)的定义,分段讨论即可求出;
(Ⅱ)先把g(x)=x-f(x)表示出来,由g(x)的表达式可作出其图象;
(Ⅲ)数形结合:方程g(x)-loga(x- )=0(a>0且a≠1)有且仅有一个实根,等价于g(x)与h(x)=
)=0(a>0且a≠1)有且仅有一个实根,等价于g(x)与h(x)=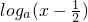 图象仅有一个交点,结合图象可得到a的限制条件,由此可求其范围.
图象仅有一个交点,结合图象可得到a的限制条件,由此可求其范围.
点评:本题考查函数作图、函数解析式的求解及函数的零点问题,本题渗透了数形结合思想、分类讨论思想.
①当0≤x<1时,f(x)=[x]=0;②当1≤x<2时,f(x)=[x]=1;
③当2≤x<3时,f(x)=[x]=2;④当3≤x<4时,f(x)=[x]=3;
所以f(x)=
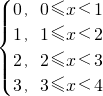 .
.(Ⅱ) g(x)=x-f(x)=
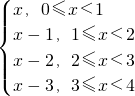 ,图象如图所示:
,图象如图所示: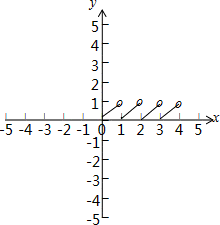
(Ⅲ)方程g(x)-
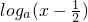 =0仅有一根等价于g(x)与h(x)=
=0仅有一根等价于g(x)与h(x)=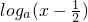 图象仅有一个交点,
图象仅有一个交点,由图象可知0<a<1 时,h(1)=
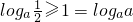 ,解得
,解得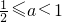 ;
;a>1时,h(2)=
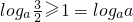 或
或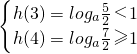 ,解得1<a≤
,解得1<a≤ 或
或 .
.综上,a的范围是[
 ,1)∪(1,
,1)∪(1, ]∪(
]∪( ,
, ].
].分析:(Ⅰ)按照f(x)的定义,分段讨论即可求出;
(Ⅱ)先把g(x)=x-f(x)表示出来,由g(x)的表达式可作出其图象;
(Ⅲ)数形结合:方程g(x)-loga(x-
 )=0(a>0且a≠1)有且仅有一个实根,等价于g(x)与h(x)=
)=0(a>0且a≠1)有且仅有一个实根,等价于g(x)与h(x)=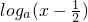 图象仅有一个交点,结合图象可得到a的限制条件,由此可求其范围.
图象仅有一个交点,结合图象可得到a的限制条件,由此可求其范围.点评:本题考查函数作图、函数解析式的求解及函数的零点问题,本题渗透了数形结合思想、分类讨论思想.

练习册系列答案
相关题目