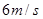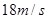题目内容
已知函数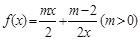 .
.
(1)若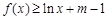 在
在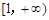 上恒成立,求m取值范围;
上恒成立,求m取值范围;
(2)证明:2 ln2 + 3 ln3+…+ n lnn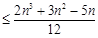 (
(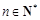 ).
).
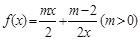 .
.(1)若
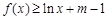 在
在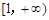 上恒成立,求m取值范围;
上恒成立,求m取值范围;(2)证明:2 ln2 + 3 ln3+…+ n lnn
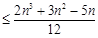 (
(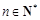 ).
). 解:令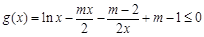 在
在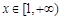 上恒成立
上恒成立
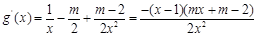 4分
4分
(1) 当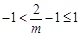 时,即
时,即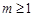 时
时
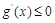 在
在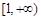 恒成立.
恒成立.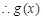 在其上递减.
在其上递减.
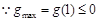
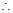 原式成立.
原式成立.
当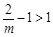 即0<m<1时
即0<m<1时
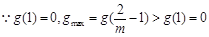
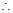 不能恒成立.
不能恒成立.
综上: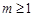 9分
9分
(2) 由 (1) 取m=1有lnx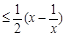
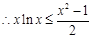 令x=n
令x=n
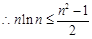
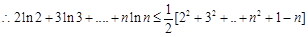
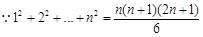
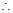 化简证得原不等式成立. 12分
化简证得原不等式成立. 12分
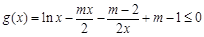 在
在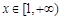 上恒成立
上恒成立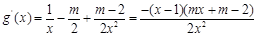 4分
4分(1) 当
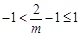 时,即
时,即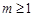 时
时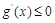 在
在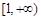 恒成立.
恒成立.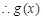 在其上递减.
在其上递减.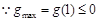
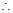 原式成立.
原式成立.当
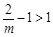 即0<m<1时
即0<m<1时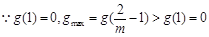
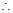 不能恒成立.
不能恒成立.综上:
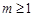 9分
9分(2) 由 (1) 取m=1有lnx
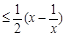
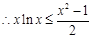 令x=n
令x=n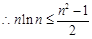
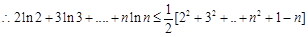
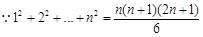
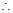 化简证得原不等式成立. 12分
化简证得原不等式成立. 12分本试题主要是考查了导数在研究函数中的运用。利用导数证明不等式的恒成立问题,以及研究函数的最值的综合运用。
(1)因为若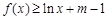 在
在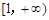 上恒成立,求m取值范围;那么关键是求解函数的最小值恒大于等于零即可。
上恒成立,求m取值范围;那么关键是求解函数的最小值恒大于等于零即可。
(2)由 (1) 取m=1有lnx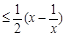 ,利用放缩法得到
,利用放缩法得到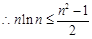 ,然后求和证明结论。
,然后求和证明结论。
解:令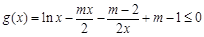 在
在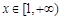 上恒成立
上恒成立
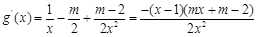 4分
4分
(1) 当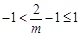 时,即
时,即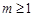 时
时
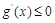 在
在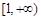 恒成立.
恒成立.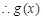 在其上递减.
在其上递减.
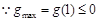
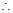 原式成立.
原式成立.
当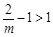 即0<m<1时
即0<m<1时
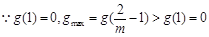
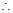 不能恒成立.
不能恒成立.
综上: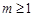 9分
9分
(2) 由 (1) 取m=1有lnx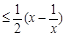
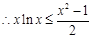 令x=n
令x=n
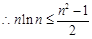
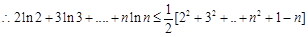
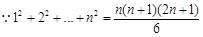
 化简证得原不等式成立. 12分
化简证得原不等式成立. 12分
(1)因为若
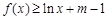 在
在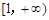 上恒成立,求m取值范围;那么关键是求解函数的最小值恒大于等于零即可。
上恒成立,求m取值范围;那么关键是求解函数的最小值恒大于等于零即可。(2)由 (1) 取m=1有lnx
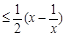 ,利用放缩法得到
,利用放缩法得到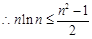 ,然后求和证明结论。
,然后求和证明结论。解:令
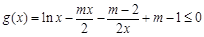 在
在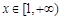 上恒成立
上恒成立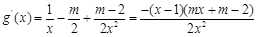 4分
4分(1) 当
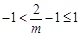 时,即
时,即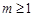 时
时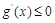 在
在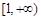 恒成立.
恒成立.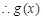 在其上递减.
在其上递减.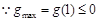
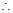 原式成立.
原式成立.当
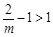 即0<m<1时
即0<m<1时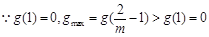
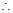 不能恒成立.
不能恒成立.综上:
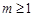 9分
9分(2) 由 (1) 取m=1有lnx
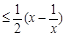
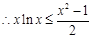 令x=n
令x=n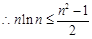
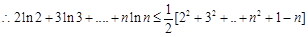
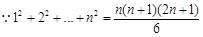
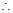 化简证得原不等式成立. 12分
化简证得原不等式成立. 12分
练习册系列答案
相关题目
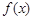 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=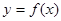 的图象在点(1,
的图象在点(1,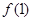 )处的切线方程是
)处的切线方程是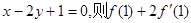 的值是( )
的值是( ) 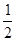
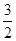
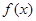 为定义在
为定义在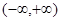 上的可导函数,且
上的可导函数,且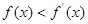 对于任意
对于任意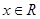 恒成立,则( )
恒成立,则( ) 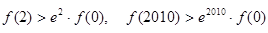
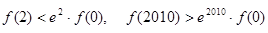
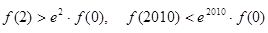
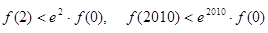
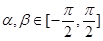 ,且
,且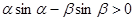 ,则下面结论正确的是( )
,则下面结论正确的是( )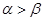
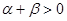
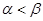
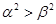
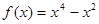 ,那么
,那么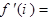 ( ) (i是虚数单位)
( ) (i是虚数单位)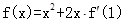 ,则
,则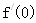 的值为( )
的值为( )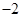
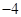
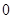

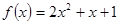 求
求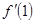
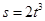 运动,则在
运动,则在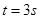 时的瞬时速度为
时的瞬时速度为