题目内容
已知二次函数f(x)=ax2+bx+c,且 f(2+x)=f(2-x),且f(x)>0的解集为(-2,c).
(Ⅰ)求f(x)的解析式.
(Ⅱ)求f(x)在区间[m,m+1]的最大值记为h(m),并求h(m)的最大值.
(Ⅰ)求f(x)的解析式.
(Ⅱ)求f(x)在区间[m,m+1]的最大值记为h(m),并求h(m)的最大值.
分析:(Ⅰ)利用f(2+x)=f(2-x),推出函数的对称轴,f(x)>0的解集为(-2,c),判断a 的符号,推出方程组,求出a、b、c,即可求解f(x)的解析式.
(Ⅱ)求出f(x)在区间[m,m+1]的最大值记为h(m)的表达式,然后画出h(m)的图象即可求出它的最大值.
(Ⅱ)求出f(x)在区间[m,m+1]的最大值记为h(m)的表达式,然后画出h(m)的图象即可求出它的最大值.
解答:(本小题共12分)
解:(Ⅰ)∵f(2+x)=f(2-x),∴函数的对称轴为x=2,
∵二次函数f(x)=ax2+bx+c,
∴-
=2…①,
又f(x)>0的解集为(-2,c).
∴ax2+bx+c=0的两个根是-2,c;并且a<0.
即4a-2b+c=0…②,ac2+bc+c=0…③,
解①②③,解得a=-
,b=2,c=6.
∴函数的解析式为:f(x)=-
x2+2x+6.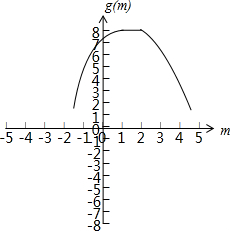
(Ⅱ)f(x)在区间[m,m+1]的最大值记为h(m),
当m+1<2即m<1时,
f(x)=-
x2+2x+6,在[m,m+1]上函数是增函数,
函数的最大值为f(m+1)=-
m2+m+
.
当m>2时,
f(x)=-
x2+2x+6,在[m,m+1]上函数是减函数,
函数的最大值为f(m)=-
m2+2m+6.
当m≤2≤m+1即1≤m≤2时,
f(x)=-
x2+2x+6,在[m,m+1]上函数的最大值为f(2)=8.
综上:h(m)=
,
函数h(m)的图象为:
所以函数h(m)的最大值为8.
解:(Ⅰ)∵f(2+x)=f(2-x),∴函数的对称轴为x=2,
∵二次函数f(x)=ax2+bx+c,
∴-
| b |
| 2a |
又f(x)>0的解集为(-2,c).
∴ax2+bx+c=0的两个根是-2,c;并且a<0.
即4a-2b+c=0…②,ac2+bc+c=0…③,
解①②③,解得a=-
| 1 |
| 2 |
∴函数的解析式为:f(x)=-
| 1 |
| 2 |

(Ⅱ)f(x)在区间[m,m+1]的最大值记为h(m),
当m+1<2即m<1时,
f(x)=-
| 1 |
| 2 |
函数的最大值为f(m+1)=-
| 1 |
| 2 |
| 15 |
| 2 |
当m>2时,
f(x)=-
| 1 |
| 2 |
函数的最大值为f(m)=-
| 1 |
| 2 |
当m≤2≤m+1即1≤m≤2时,
f(x)=-
| 1 |
| 2 |
综上:h(m)=
|
函数h(m)的图象为:
所以函数h(m)的最大值为8.
点评:本题考查二次函数闭区间上的最大值的求法,函数的解析式的求法,考查转化思想以及计算能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目