Question

如图，矩形ABCD中，AC=8，AB边上一点P满足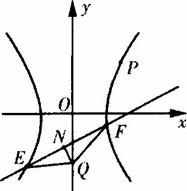，若离心率为2的双曲线C以矩形的对角线所在直线为渐近线，且经过点P.

(Ⅰ)求双曲线C的标准方程；

(Ⅱ)若直线y=kx+m(k≠0，m≠0)与双曲线C交于不同的两点E、F，且E、F两点都在以Q(0，-3)为圆心的同一圆上，求实数m的取值范围.

Answer 1

解：(Ⅰ)因为双曲线C的离心率为2,所以可设双曲线C的方程为=l,

由此可得渐近线的斜率k=±∠BOx=60°,又OB=4从而B(2,),A(2,). 

又因=3,故P(2,),代入双曲线方程得a²=3,故双曲线C的方程为：=1. 

(Ⅱ)如图所示,由方程组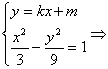(k²-3)x²+2kmx+m²+9=0

设E(x₁,y₁)、F(x₂,y₂),线段EF的中点为N(x₀,y₀),则有

,①

由韦达定理得x₀=,y₀=kx₀+m=.  

因为E、F两点都在以Q(0,-3)为圆心的同一圆上,所以NQ⊥EF,即

k_NQ=3k²=4m+9.②

由①,②得m＞4或＜m＜0.