题目内容
（2012•盐城一模）设椭圆C：
+
=1(a＞b＞0)恒过定点A（1，2），则椭圆的中心到准线的距离的最小值
+2
+2．
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 5 |
分析：根据椭圆C：
+
=1(a＞b＞0)恒过定点A（1，2），可得
+
=1，利用椭圆几何量之间的关系，设
=
，等式可转化为t2a4-（t2+1）a2+5=0，利用判别式，即可求得椭圆的中心到准线的距离的最小值．
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 4 |
| b2 |
| a2 |
| c |
| 1 |
| t |
解答：解：设椭圆的焦距为2c，同时可设
=
，∴c=ta2
∵椭圆C：
+
=1(a＞b＞0)恒过定点A（1，2），
∴
+
=1
∴b2+4a2=a2b2
∴5a2-c2=a2（a2-c2）
∴5a2-（ta2）2=a2[a2-（ta2）2]
∴t2a4-（t2+1）a2+5=0
∴△=（t2+1）2-20t2≥0时，方程有解
∴t2-2
t+1≥0
∴t≥
+2，或0＜t≤
-2
∴0＜
≤
-2，或
≥
+2
∵椭圆C：
+
=1(a＞b＞0)恒过定点A（1，2），
∴椭圆的中心到准线x=
＞1
∴椭圆的中心到准线的距离的最小值
+2
故答案为：
+2
| a2 |
| c |
| 1 |
| t |
∵椭圆C：
| x2 |
| a2 |
| y2 |
| b2 |
∴
| 1 |
| a2 |
| 4 |
| b2 |
∴b2+4a2=a2b2
∴5a2-c2=a2（a2-c2）
∴5a2-（ta2）2=a2[a2-（ta2）2]
∴t2a4-（t2+1）a2+5=0
∴△=（t2+1）2-20t2≥0时，方程有解
∴t2-2
| 5 |
∴t≥
| 5 |
| 5 |
∴0＜
| 1 |
| t |
| 5 |
| 1 |
| t |
| 5 |
∵椭圆C：
| x2 |
| a2 |
| y2 |
| b2 |
∴椭圆的中心到准线x=
| a2 |
| c |
∴椭圆的中心到准线的距离的最小值
| 5 |
故答案为：
| 5 |
点评：本题综合考查椭圆的标准方程与性质，考查解不等式，考查学生分析解决问题的能力，有一定的技巧．
练习册系列答案
阅读快车系列答案
相关题目
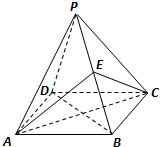（2012•盐城一模）如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PA=PC，E为PB的中点．