题目内容
13.已知函数f(x)=2ax2+4x-3-a,a∈R.(1)当a=1时,求函数f(x)在[-1,1]上的最大值;
(2)如果函数f(x)在区间[-1,1]上存在两个不同的零点,求a的取值范围.
分析 (1)当a=1时,则f(x)=2x2+4x-4=2(x2+2x)-4=2(x+1)2-6,由此可得f(x)的最大值f(1)的值.
(2)当a=0时,经检验满足条件.当a≠0时,令△=0求得a=-1,a=-2,经检验都满足条件.
当f(-1)•f(1)≤0时,求出a的取值范围.当y=f(x)在区间[-1,1]上有两个零点时,
利用二次函数的性质求得实数a的取值范围.再把以上实数a的取值范围取并集,即得所求.
解答 解:(1)当a=1时,则f(x)=2x2+4x-4=2(x2+2x)-4=2(x+1)2-6.
因为x∈[-1,1],所以x=1时,f(x)的最大值f(1)=2.…(3分)
(2),若a=0时,f(x)=4x-3,显然在区间[-1,1]上有零点,所以a=0时,命题不成立.…(4分)
若a≠0时,令△=16+8a(3+a)=8(a+1)(a+2)=0,解得a=-1,a=-2. …(5分)
①当a=-1时,f(x)=-2x2+4x-2=-2(x-1)2,f(x)的零点为 x=1,满足条件.
②当 a=-2时,f(x)=-4x2+4x-1=-4(x-$\frac{1}{2}$)2,求得函数的零点 x=$\frac{1}{2}$,满足条件.
所以当 a=0,-1,-2时,y=f(x)均恰有一个零点在区间[-1,1]上.…(7分)
③当f(-1)•f(1)=(a-7)(a+1)≤0,即-1≤a≤7时,
y=f(x)在区间[-1,1]上必有零点.…(8分)
④若y=f(x)在区间[-1,1]上有两个零点,则$\left\{\begin{array}{l}a>0\\△=8(a+1)(a+2)>0\\-1<-\frac{1}{a}<1\\ f(-1)≥0\\ f(1)≥0\end{array}\right.$,
或$\left\{\begin{array}{l}a<0\\△=8(a+1)(a+2)>0\\-1<-\frac{1}{a}<1\\ f(-1)≤0\\ f(1)≤0\end{array}\right.$.…(12分)
解得a≥7或a<-2.
综上所述,函数f(x)在区间[-1,1]上存在极值点,实数a的取值范围是{a|a≥-1,或a≤-2},
故答案为 {a|0>a≥-1,或a≤-2或a>0}.…(13分)
点评 本题主要考查求二次函数在闭区间上的最值,求函数的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 10与8 | B. | 10与4 | C. | 8与10 | D. | 4与10 |
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | a | b | $\frac{1}{24}$ |
(2)求m的值;
(3)求ξ的数学期望.
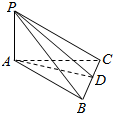 如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.
如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.