题目内容
17. 如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=4,则抛物线的方程为( )
如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=4,则抛物线的方程为( )| A. | y2=8x | B. | y2=4x | C. | y2=2x | D. | y2=x |
分析 分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,根据抛物线定义可知|BD|=a,进而推断出∠BCD的值,在直角三角形中求得a,进而根据BD∥FG,利用比例线段的性质可求得p,则抛物线方程可得.
解答 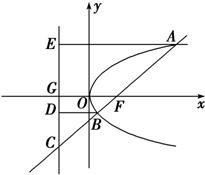 解:如图分别过点A,B作准线的垂线,分别交准线于点E,D,
解:如图分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则由已知得:|BC|=2a,
由定义得:|BD|=a,故∠BCD=30°,
在直角三角形ACE中,∵|AF|=4,|AC|=4+3a,
∴2|AE|=|AC|
∴4+3a=8,
从而得a=$\frac{4}{3}$,
∵BD∥FG,
∴$\frac{\frac{4}{3}}{p}$=$\frac{2}{3}$求得p=2,
因此抛物线方程为y2=4x.
故选:B.
点评 本题主要考查了抛物线的简单性质.考查了学生对抛物线的定义和基本知识的综合把握.

练习册系列答案
相关题目
8.若p,q都为命题,则“p或q为真命题”是“?p且q为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5. 用红、黄、蓝、白、黑五种颜色涂在“田”字形的4个小方格内,每格涂一种颜色,相邻两格(有公共变边)涂不同的颜色,如果颜色可以反复使用,则所有涂色方法的种数为( )
用红、黄、蓝、白、黑五种颜色涂在“田”字形的4个小方格内,每格涂一种颜色,相邻两格(有公共变边)涂不同的颜色,如果颜色可以反复使用,则所有涂色方法的种数为( )
 用红、黄、蓝、白、黑五种颜色涂在“田”字形的4个小方格内,每格涂一种颜色,相邻两格(有公共变边)涂不同的颜色,如果颜色可以反复使用,则所有涂色方法的种数为( )
用红、黄、蓝、白、黑五种颜色涂在“田”字形的4个小方格内,每格涂一种颜色,相邻两格(有公共变边)涂不同的颜色,如果颜色可以反复使用,则所有涂色方法的种数为( )| A. | 120 | B. | 240 | C. | 260 | D. | 360 |
9.已知$f(x)=cos({2ωx+\frac{π}{4}})({x∈R,ω>0})$的最小正周期为π,将y=f(x)的图象上所有的点的横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标不变;再把所得的图象向右平移|φ|个单位长度,所得的图象关于原点对称,则φ的一个值是( )
| A. | $\frac{3π}{16}$ | B. | $\frac{5π}{16}$ | C. | $\frac{3π}{4}$ | D. | $\frac{3π}{8}$ |
6.在△ABC中,已知∠ACB=90°,CA=3,CB=4,点E是边AB的中点,则$\overrightarrow{CE}$•$\overrightarrow{AB}$=( )
| A. | 2 | B. | $\frac{7}{2}$ | C. | $\sqrt{7}$ | D. | -$\frac{7}{2}$ |
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.