题目内容
6．在△ABC中，已知∠ACB=90°，CA=3，CB=4，点E是边AB的中点，则$\overrightarrow{CE}$•$\overrightarrow{AB}$=（ ）| A． | 2 | B． | $\frac{7}{2}$ | C． | $\sqrt{7}$ | D． | -$\frac{7}{2}$ |
分析 根据已知条件便可得到，$\overrightarrow{CE}=\frac{1}{2}（\overrightarrow{CA}+\overrightarrow{CB}）$，$\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$，带入$\overrightarrow{CE}•\overrightarrow{AB}$进行数量积的运算即可得到答案．
解答 
解：如图，
E是AB中点；
∴$\overrightarrow{CE}=\frac{1}{2}（\overrightarrow{CB}+\overrightarrow{CA}）$，$\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$；
∴$\overrightarrow{CE}•\overrightarrow{AB}=\frac{1}{2}（{\overrightarrow{CB}}^{2}-{\overrightarrow{CA}}^{2}）$=$\frac{7}{2}$．
故选：B．
点评 考查向量加法的平行四边形法则，向量减法的几何意义，以及数量积的运算．
练习册系列答案
相关题目
16．“m＞2”是“双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
17．
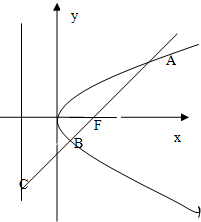如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=4，则抛物线的方程为（ ）
如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=4，则抛物线的方程为（ ）| A． | y2=8x | B． | y2=4x | C． | y2=2x | D． | y2=x |
14．不等式|x-1|+|x+2|≤4的解集是（ ）
| A． | $（-\frac{5}{2}，\frac{3}{2}）$ | B． | $[-\frac{5}{2}，\frac{3}{2}]$ | C． | $[-2，\frac{3}{2}]$ | D． | $[-\frac{5}{2}，1）$ |
1．某市为缓解交通压力，计划在某路段实施“交通限行”，为了解公众对该路段“交通限行”的态度，某机构从经过该路段的人员中随机抽查了40人进行调查，将调查情况进行整理，制成如表：
（Ⅰ）如果经过该路段人员对“交通限行”的赞成率为0.45，则x的值为；
（Ⅱ）在（Ⅰ）的条件下，若从年龄在[45，60），[60，75）两组赞成“交通限行”的人中再随机选取2人进行进一步的采访，记选中的2人至少有1人来自[60，75）年龄段为事件M，求事件M的概率．
| 年龄（岁） | [15，30） | [30，45） | [45，60） | [60，75） |
| 人数 | 12 | 13 | 8 | 7 |
| 赞成人数 | 5 | 7 | x | 3 |
（Ⅱ）在（Ⅰ）的条件下，若从年龄在[45，60），[60，75）两组赞成“交通限行”的人中再随机选取2人进行进一步的采访，记选中的2人至少有1人来自[60，75）年龄段为事件M，求事件M的概率．