题目内容
5．
用红、黄、蓝、白、黑五种颜色涂在“田”字形的4个小方格内，每格涂一种颜色，相邻两格（有公共变边）涂不同的颜色，如果颜色可以反复使用，则所有涂色方法的种数为（ ）| A． | 120 | B． | 240 | C． | 260 | D． | 360 |
分析 先考虑所有可能的情况：①当1与4的颜色相同时，先排1，有5种结果，再排2，有4种结果，4与1相同，最后排3，有4种结果，
②当1与4的颜色不同时，类似利用乘法原理，最后根据分类计数原理得到结果；
解答 解：①当1与4的颜色相同时，先排1，有5种结果，再排2，有4种结果，4与1相同，最后排3，有3种结果，共有C51C41C41=80种结果
②当1与4的颜色不同时，有C51C41C31C31=180种结果，
根据分类计数原理知共有80+180=260，
故选：C．
点评 本题考查分类计数原理的问题，注意对于复杂一点的计数问题，有时分类以后，每类方法并不都是一步完成的，必须在分类后又分步，综合利用两个原理解决．
练习册系列答案
53随堂测系列答案
相关题目
16．“m＞2”是“双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
10．某年级有1000名学生，现从中抽取100人作为样本，采用系统抽样的方法，将全体学生按照1～1000编号，并按照编号顺序平均分成100组（1～10号，11～20号，…，991～1000号）．若从第1组抽出的编号为6，则从第10组抽出的编号为（ ）
| A． | 86 | B． | 96 | C． | 106 | D． | 97 |
17．
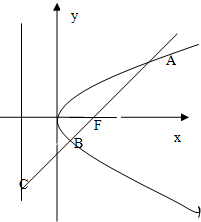如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=4，则抛物线的方程为（ ）
如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=4，则抛物线的方程为（ ）| A． | y2=8x | B． | y2=4x | C． | y2=2x | D． | y2=x |
14．不等式|x-1|+|x+2|≤4的解集是（ ）
| A． | $（-\frac{5}{2}，\frac{3}{2}）$ | B． | $[-\frac{5}{2}，\frac{3}{2}]$ | C． | $[-2，\frac{3}{2}]$ | D． | $[-\frac{5}{2}，1）$ |