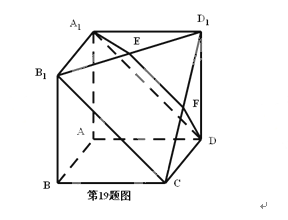
题目内容
【题目】(2015·陕西)设fn(x)是等比数列1,x,x2...,xn的各项和,其中x>0,n![]() N, ,n≥2,
N, ,n≥2,
(1)证明:函数Fn(x)=fn(x)-2在(![]() ,1)内有且仅有一个零点(记为xn),且xn=
,1)内有且仅有一个零点(记为xn),且xn=![]() +
+![]() xnn+1;
xnn+1;
(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)与gn(x)的大小,并加以证明.
【答案】
(1)
见解析。
(2)
见解析。
【解析】(I)Fn(x)=fn(x)-2=1+x+x2+...+xn-2则Fn(1)=n-1>0
Fn(![]() )=1+
)=1+![]() +(
+(![]() )2+...+(
)2+...+(![]() )n-2=
)n-2=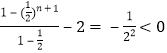
所以Fn(x)在(![]() ,1)内至少存在一个零点xn.
,1)内至少存在一个零点xn.
又Fn'(x)=1+2x+...+nxn-1>0,故在(![]() ,1)内单调递增,
,1)内单调递增,
所以Fn(x)在(![]() ,1内有且仅有一个零点xn.
,1内有且仅有一个零点xn.
因为xn是Fn(x)的零点,所以Fn(xn)=0,即![]() -2=0,故xn=
-2=0,故xn=![]() +
+![]() xnn+1.
xnn+1.
(II)解法一:由题设,gn(x)=![]()
设h(x)= fn(x)-gn(x)=1+x+x2+...+xn-![]() ,
,
x>0, 当x=1时, fn(x)=gn(x)
当x≠1时, h'(x)=1+2x+...nxn-1-![]()
若0<x<1,h'(x)>xn-1+2xn-1+...+nxn-1-![]() =
=![]() -
-![]() =0
=0
若x>1,h'(x)<xn-1+2xn-1+...+nxn-1-![]() =
=![]() -
-![]() =0
=0
所以h(x)在(0,1)上递增,在(1,+![]() )上递减,
)上递减,
所以h(x)<h(1)=0,即fn(x)<gn(x)
综上所述,当x=1时, fn(x)=gn(x);当x≠1时fn(x)<gn(x)
解法二 由题设, fn(x)=1+x+x2+...+xn, gn(x)=![]() , x>0
, x>0
当x=1时, fn(x)=gn(x)
当x≠1时, 用数学归纳法可以证明fn(x)<gn(x).
当n=2时, f2(x)-g2(x)=-![]() (1-x)2<0所以f2(x)<g2(x)成立.
(1-x)2<0所以f2(x)<g2(x)成立.
假设n=k(k≥2)时,不等式成立,即fk(x)<gk(x)
那么,当n=k+1时,
.fk+1(x)=fk(x)+xk+1<gk(x)+xk+1=![]() +xk+1=
+xk+1=![]()
又gk+1(x)-![]() =
=![]()
令fk(x)=kxk+1-(k+1)xk , +1(x>0), 则hk'(x)=k(k+1)xk-k(k+1)xk-1(x-1)
所以当0<x<1,hk'(x)<0, hk'(x)在(0,1)上递减;
当x>1,hk'(x)>0,hk(x)在(1,+![]() )上递增.
)上递增.
所以hk(x)>hk(1)=0,从而gk+1(x)>![]()
故fk+1(x)<gk+1(x).即n=k+1,不等式也成立.
所以,对于一切n≥2的整数,都有.fn(x)<gn(x)
解法三:由已知,记等差数列为{ak}, 等比数列为,则,,{bk} k=1,2,...,n+1, 则a1=b1=1, an+1=bn+1=xn
所以,ak=1+(k-1)-![]() (2≤k≤n), bk=xk-1(2≤k≤n)
(2≤k≤n), bk=xk-1(2≤k≤n)
令mk(x)=ak-bk=1+![]() -xk-1(2≤k≤n).
-xk-1(2≤k≤n).
当x=1时, ak=bk,所以fn(x)=gn(x)
当x≠1时, mk'(x)=![]() nxn-1-(k-1)xk-2=(k-1)xk-2(xn-k+1-1)
nxn-1-(k-1)xk-2=(k-1)xk-2(xn-k+1-1)
而2≤k≤n,,所以k-1>0,n-k+1≥1.
若0<x<1 , xn-k+1<1, mk'(x)<0
当x>1, ,,, xn-k+1>1,mk'(x)>0
从而mk(x)在(0,1)上递减,mk(x)在(1,+![]() )上递增.所以,mk(x)>mk(1)=0
)上递增.所以,mk(x)>mk(1)=0
所以当x>0又a1=b1),an+1=bn+1 , 故fn(x)<gn(x)
综上所述,当x=1时, fn(x)=gn(x);当x≠1时fn(x)<gn(x)。
【考点精析】解答此题的关键在于理解等比数列的前n项和公式的相关知识,掌握前![]() 项和公式:
项和公式: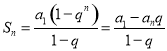 .
.