题目内容
【题目】如图所示，在多面体A1B1D1-DCBA中,四边形AA1B1B，ADD1A1,ABCD均为正方形，E为B1D1的中点 ，过A1 ， D，E的平面交CD 1于F。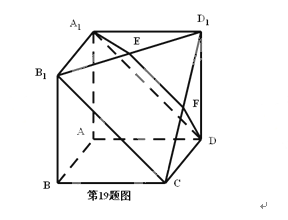
（1）证明：EF∥B1C
（2）求二面角E-A1D-B1的余弦。
【答案】
（1）
证明：依据正方形的性质可知A1B1//AB//DC,且A1B1=AB=DC,从而A1B1CD为平行四边形，则B1C//A1D,根据线面平行的判断定理知B1C//面A1DE，再由线面平行性质定理知EF//B1C.
（2）
解：因为四边形AA1B1B,ADD1A1,ABCD均为正方形，所以AA1
AB,AA1AD,ADAB,且AA1=AB=AD，可以建以A为原点，分别为
,
，
为x轴，y轴，z轴单位正向量的平面直角坐标系，写出相关点的坐标，设出面A1DE的法向量
=(r1,s1,t1)由此得r1,s1,t1应满足方程组
,(-1,1)尾气中一组解，所以可取
=(-1,1,1),同理A1B1CD的法向量
=（0,1，1）所以结合图形知二面角E-A1D-B的余弦值
=
【解析】
（2）因为四边形AA1B1B,ADD1A1,ABCD均为正方形，所以AA1AB,AA1AD,ADAB,且AA1=AB=AD，可以建以A为原点，分别为,，为x轴，y轴，z轴单位正向量的平面直角坐标系，写出相关点的坐标，设出面A1DE的法向量=(r1,s1,t1)由此得r1,s1,t1应满足方程组
,(-1,1)为其中一组解，所以可取=(-1,1,1),同理A1B1CD的法向量=（0,1，1）所以结合图形知二面角E-A1D-B的余弦值
=。
【考点精析】关于本题考查的向量语言表述线面的垂直、平行关系，需要了解要证明一条直线和一个平面平行，也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线
的方向向量是
，平面
内的两个相交向量分别为
，若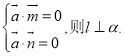
才能得出正确答案．
