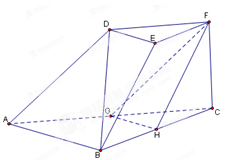
题目内容
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() 且点
且点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点
的中点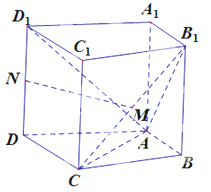
(1)求证:![]() 平面
平面![]()
(2)求二面角![]() 的正弦值
的正弦值
(3)设![]() 为棱
为棱![]() 上的点,若直线
上的点,若直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长
的长
【答案】
(1)
见解答
(2)
![]()
(3)
![]()
【解析】如图,以![]() 为原点建立空间直角坐标系,依题意可得
为原点建立空间直角坐标系,依题意可得![]() ,又因为
,又因为![]() 分别为
分别为![]() 和
和![]() 的中点,得
的中点,得![]()
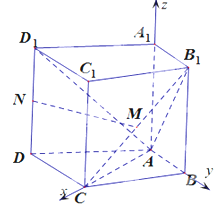
(1)证明:依题意,可得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,![]() ,由此可得,
,由此可得,![]() ,又因为直线
,又因为直线![]()
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(2)![]() ,设
,设![]() 为平面
为平面![]() 的法向量,则
的法向量,则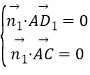 ,即
,即![]() ,不妨设
,不妨设![]() ,可得
,可得![]() 。
。
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则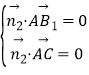 ,又
,又![]() ,得
,得![]() ,不妨设
,不妨设![]() ,可得
,可得![]() 因此有
因此有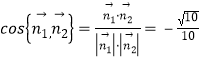 ,于是
,于是![]() ,所以二面角
,所以二面角![]() 的正弦值为
的正弦值为![]() 。
。
(3)依题意,可设![]() ,其中
,其中![]() 则
则![]() 从而
从而![]() 又
又![]() 为平面
为平面![]() 的一个法向量,由已知得
的一个法向量,由已知得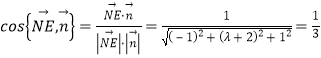 整理得
整理得![]() 又因为
又因为![]() ,解得
,解得![]() 所以线段
所以线段![]() 的长为
的长为![]()
【考点精析】利用空间向量的定义对题目进行判断即可得到答案,需要熟知在空间,具有大小和方向的量称为空间向量.

练习册系列答案
相关题目
【题目】(2015·陕西)随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.