题目内容
11.是否存在同时满足下列条件的双曲线,若存在,求出其方程;若不存在,说明理由.(1)渐近线方程是x±2y=0;
(2)点A(5,0)到双曲线上的动点P的距离的最小值为$\sqrt{6}$.
分析 根据双曲线和其渐近线之间的关系,设出双曲线的方程,根据点A(5,0)到双曲线上动点P的距离最小值为$\sqrt{6}$,转化为双曲线与半径为$\sqrt{6}$的圆A相切,联立消去y得,利用△=0即可求得双曲线的方程.
解答 解:由渐近线方程为x±2y=0,设双曲线方程为x2-4y2=m,
∵点A(5,0)到双曲线上动点P的距离的最小值为$\sqrt{6}$,
说明双曲线与半径为$\sqrt{6}$的圆A相切,
圆A方程为(x-5)2+y2=6,与x2-4y2=m联立消去y得:4(x-5)2+x2=24+m
化简得到:5x2-40x+76-m=0,△=402-4×5×(76-m)=0,
解得m=-4 所以满足条件的双曲线方程为x2-4y2=-4,
即y2-$\frac{{x}^{2}}{4}$=1.
或者双曲线的顶点在(5+$\sqrt{6}$,0)渐近线为x±2y=0,双曲线方程为:$\frac{{x}^{2}}{31+10\sqrt{6}}-\frac{4{y}^{2}}{31+10\sqrt{6}}$=1.
所以所求双曲线方程为:y2-$\frac{{x}^{2}}{4}$=1,$\frac{{x}^{2}}{31+10\sqrt{6}}-\frac{4{y}^{2}}{31+10\sqrt{6}}$=1.
点评 考查双曲线的简单的几何性质,特别是双曲线方程与其渐近线方程之间的关系,此题设双曲线方程为x2-4y2=m,避免了讨论,条件(2)的设置增加了题目的难度,体现了转化的思想,属中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
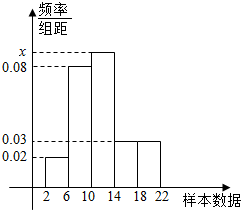 为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为680.
为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为680.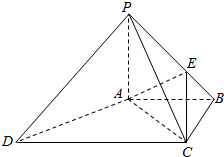 如图,四棱锥P-ABCD中,PA⊥底面ABCD,CD=2,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,CD=2,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,点E在棱PB上,且PE=2EB.