题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）．
（1）若椭圆的离心率为 
，且点（1， ）在椭圆上，
①求椭圆的方程；
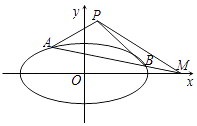
②设P（﹣1，﹣ ），R、S分别为椭圆C的右顶点和上顶点，直线PR和PS与y轴和x轴相交于点M，N，求直线MN的方程．
（2）设D（b，0），过D点的直线l与椭圆C交于E、F两点，且E、F均在y轴的右侧， 
=2 
，求椭圆离心率的取值范围．
【答案】
（1）解：①∵椭圆C： 
=1（a＞b＞0），椭圆的离心率为 
，且点（1， ）在椭圆上，
∴ 
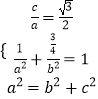，解得a=2，b=1，
∴椭圆的方程为 
=1．
②P（﹣1，﹣ ），R、S分别为椭圆C： =1的右顶点和上顶点，直线PR和PS与y轴和x轴相交于点M，N，
∴R（2，0），S（0，1），
∴直线PR： 
，即 
x﹣6y﹣2 =0，∴M（0，﹣ 
），
直线PS： 
，即（ 
）x﹣2y+2=0，∴N（2 ﹣4，0），
∴直线MN的方程为： 
，即y=﹣ 
．
（2）设E（x1，y1），F（x2，y2），∵ 
，∴ 
．
根据题意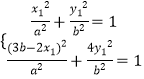 
，解得 
，
连SD，延长交椭圆于点Q．
直线SD的方程为x+y﹣b=0，代入椭圆方程解得Q点的横坐标 
，
所以， 
，即a4﹣4a2b2+3b4＜0，
解得b2＜a2＜3b2，即a2＜3（a2﹣c2），
∴ 
＜ 
， 
．
∴椭圆离心率e的取值范围为（0， 
）．
【解析】（1）①由题意可得含有a，b，c的方程组，解方程组可得a，b的值，从而可得椭圆的方程；②先求出点R，S的坐标，再求出直线PR，直线PS的方程，进而可得点M，N的坐标，从而可得直线MN的方程．（2）先设点E，F的坐标，联立方程组可解得x1，再连结SD，延长交椭圆于点Q，求出直线SD的方程，代入椭圆方程可解得xQ，进而可得含有a，c的不等式，从而可得椭圆离心率的取值范围．
