题目内容
【题目】某校命制了一套调查问卷（试卷满分均为100分），并对整个学校的学生进行了测试.现从这些学生的成绩中随机抽取了50名学生的成绩，按照
分成5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）.
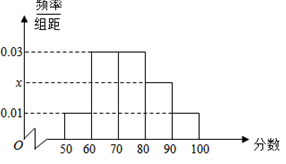
（1）求频率分布直方图中x的值，并估计所抽取的50名学生成绩的平均数、中位数（同一组中的数据用该组区间的中点值代表）；
（2）用样本估计总体，若该校共有2000名学生，试估计该校这次测试成绩不低于70分的人数；
（3）若利用分层抽样的方法从样本中成绩不低于70分的学生中抽取6人，再从这6人中随机抽取3人，试求成绩在
的学生至少有1人被抽到的概率.
【答案】（1）
，74，
；（2）1200；（3）
.
【解析】
（1）根据频率和为
可求得第第
组的频率，由此求得
的值；根据频率分布直方图中平均数和中位数的估计方法可计算得到结果；
（2）计算得到
名学生中成绩不低于
分的频率，根据样本估计总体的方法，利用总数
频率可得所求人数；
（3）根据分层抽样原则确定
、
和
种分别抽取的人数，采用列举法列出所有结果，从而可知成绩在
的学生没人被抽到的概率；根据对立事件概率公式可求得结果.
（1）由频率分布直方图可得第组的频率为：
估计所抽取的名学生成绩的平均数为：
由于前两组的频率之和为
，前三组的频率之和为
中位数在第
组中
设中位数为
，则有：
，解得：
即所求的中位数为
（2）由（1）知：名学生中成绩不低于分的频率为：
用样本估计总体，可以估计高三年级
名学生中成绩不低于分的人数为：
（3）由（1）可知，后三组中的人数分别为
，
，
这三组中所抽取的人数分别为，
，
记成绩在的名学生分别为
，成绩在的名学生分别为
，成绩在的名学生为
，则从中随机抽取人的所有可能结果为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共
种
其中成绩在的学生没人被抽到的可能结果为，只有种，
故成绩在的学生至少有人被抽到的概率：
