题目内容

6．在△ABC中，$\frac{a}{cosA}$=$\frac{b}{cosB}$=$\frac{c}{sinC}$，则在△ABC中最大的角是（　　）
A．90°B．60°C．75°D．105°

分析 运用正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$，结合同角的商数关系，可得A=B=45°，再由三角形的内角和定理，可得C最大．

解答 解：由条件$\frac{a}{cosA}$=$\frac{b}{cosB}$=$\frac{c}{sinC}$，
结合正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$，
可得$\frac{sinA}{cosA}=\frac{sinB}{cosB}=\frac{sinC}{sinC}$=1，
即有tanA=tanB=1，
由A，B为三角形的内角，可得A=B=45°，
则C=90°，
故选：A．

点评 本题考查正弦定理的运用，考查同角的商数关系，属于基础题．

练习册系列答案
相关题目
16．已知抛物线C：y=-x2+4x-3．
（1）求抛物线C在点A（0，-3）和点B（3，0）处的切线的交点坐标；
（2）求抛物线C与它在点A和点B处的切线所围成的图形的面积．
17．将函数$f（x）=3cos（x+\frac{2π}{3}）$的图象向左平移$\frac{π}{3}$后，得到函数y=g（x）的图象，则f（x）的最大值为3，g（x）在区间$[{-\frac{π}{2}，\frac{π}{2}}]$上的单调递增区间为[0，$\frac{π}{2}$]．
14．已知抛物线y2=2px（p＞0）上一点P（3，t）到其焦点的距离为4．
（1）求p的值；
（2）过点Q（1，0）作两条直线l1，l2与抛物线分别交于点A、B和C、D，点M，N分别是线段AB和CD的中点，设直线l1，l2的斜率分别为k1，k2，若k1+k2=3，求证：直线MN过定点．
1．5名乒乓球队员中，有2名老队员和3名新队员，现从中选出3名队员排成1，2，3号参加团体比赛，则入选的3名队员中至少有一名老队员，且1，2号至少有1名新队员的排法有（　　）种．
A．12B．36C．48D．72
11．设两向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$满足|$\overrightarrow{{e}_{1}}$|=2，|$\overrightarrow{{e}_{2}}$|=1，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$的夹角为60°，
（1）若向量2t$\overrightarrow{{e}_{1}}$+7$\overrightarrow{{e}_{2}}$与向量$\overrightarrow{{e}_{1}}$+t$\overrightarrow{{e}_{2}}$垂直，求实数t的值；
（2）若向量2t$\overrightarrow{{e}_{1}}$+7$\overrightarrow{{e}_{2}}$与向量$\overrightarrow{{e}_{1}}$+t$\overrightarrow{{e}_{2}}$平行，求实数t的值．
18．在△ABC中，若2b=a+c，b2=ac，则△ABC的形状为（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
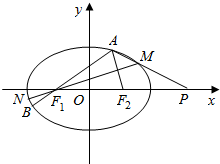3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$．A为椭圆C上一动点（A异于左、右顶点），F1、F2分别为椭圆C的左、右焦点，且△AF1F2面积的最大值为1；
（Ⅰ）求椭圆C的方程
（Ⅱ）如图，已知点P（2，0），连接AP交椭圆C于点M，连接AF1、MF1并延长分别交椭圆C于点B、N，记$\overrightarrow{A{F}_{1}}$=λ$\overrightarrow{{F}_{1}B}$，$\overrightarrow{M{F}_{1}}$=μ$\overrightarrow{{F}_{1}N}$（λ、μ∈R），求λ+μ的取值范围．
4．在△ABC中，内角A，B，C所对的边分别为a，b，c，函数f（x）=$\sqrt{3}$sinx-cosx，若f（2A）=f（2B），且A≠B．
（1）求∠C的大小；
（2）若△ABC的面积为$\frac{\sqrt{3}}{8}$，求a+b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网