题目内容
【题目】已知函数![]() .
.
(1)求![]() 的极大值点;
的极大值点;
(2)当![]() ,
,![]() 时,若过点
时,若过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切,求t的取值范围.
相切,求t的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先求导数,求出导函数的零点,安照![]() 、
、![]() 、
、![]() 三种情况讨论
三种情况讨论![]() 的极大值点;
的极大值点;
(2)设切点![]() ,利用该点的导数等于切线斜率、切线过点
,利用该点的导数等于切线斜率、切线过点![]() 两个条件整理得到关于
两个条件整理得到关于![]() 的方程
的方程![]() ,进一步研究函数
,进一步研究函数![]() 的取值情况.
的取值情况.
解:(1)![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
若![]() ,则当
,则当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
此时![]() 的极大值点为
的极大值点为![]() ;
;
若![]() ,则当
,则当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
此时![]() 的极大值点为
的极大值点为![]() ;
;
若![]() ,
,![]() 在
在![]() 上单调递增,无极值.
上单调递增,无极值.
(2)设过点![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]() ,
,
则![]() ,且切线斜率
,且切线斜率![]() ,
,
所以切线方程为![]() ,
,
因此![]() ,整理得
,整理得![]() ,
,
构造函数![]() ,
,
则“若过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切”等价于“
相切”等价于“![]() 有三个不同的零点”,
有三个不同的零点”,![]() ,
,![]() 与
与![]() 的关系如下表:
的关系如下表:
|
|
|
|
|
|
| + | 0 | 0 | + | |
|
| 极大值 |
| 极小值 |
|
所以![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,
,
要使![]() 有三个解,即
有三个解,即![]() 且
且![]() ,解得
,解得![]() .
.
因此,当过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切时,
相切时,
t的取值范围是![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某商场为提高服务质量,随机调查了60名男顾客和80名女顾客,每位顾客均对该商场的服务给出满意或不满意的评价,得到下面不完整的列联表:
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
(1)根据已知条件将列联表补充完整;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
附: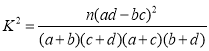
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |