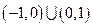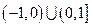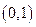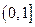题目内容
(12分) 已知函数 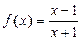 ,x ∈[ 3 , 5 ] ,
,x ∈[ 3 , 5 ] ,
(1)用定义证明函数的单调性;
(2)求函数的最大值和最小值。
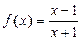 ,x ∈[ 3 , 5 ] ,
,x ∈[ 3 , 5 ] ,(1)用定义证明函数的单调性;
(2)求函数的最大值和最小值。
略
解:(1)证明:设x1,x2∈[3,5],且x1<x2
f(x1) - f(x2) =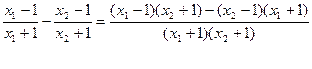
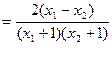
∵x1,x2∈[3,5]
∴x1+1>0 , x2+1>0
∵x1<x2
∴x1-x2<0
∴f(x1)- f(x2) <0 即f(x1) < f(x2)
∴f(x)在[3,5]为增函数。
(2)∵f(x)在[3,5]为增函数
∴当x=3时函数取最小值f(3)=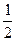
当x=5时函数取最大值f(5)=
f(x1) - f(x2) =
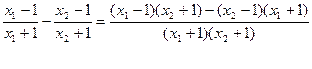
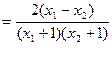
∵x1,x2∈[3,5]
∴x1+1>0 , x2+1>0
∵x1<x2
∴x1-x2<0
∴f(x1)- f(x2) <0 即f(x1) < f(x2)
∴f(x)在[3,5]为增函数。
(2)∵f(x)在[3,5]为增函数
∴当x=3时函数取最小值f(3)=
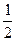
当x=5时函数取最大值f(5)=

练习册系列答案
相关题目
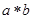 为:
为: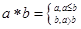 如
如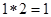 ,则函数
,则函数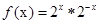 的值域为
的值域为 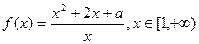 .
.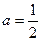 时,求函数
时,求函数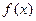 的最小值;
的最小值;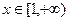 ,
,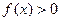 恒成立,试求实数
恒成立,试求实数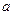 的取值范围
的取值范围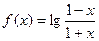
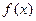 的定义域;
的定义域;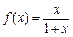 (x∈[0,3])的单调性,并证明你的结论.
(x∈[0,3])的单调性,并证明你的结论.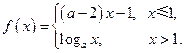 若
若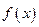 在
在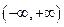 上单调递增,则实数
上单调递增,则实数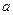 的取值范围为( )
的取值范围为( )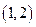 B
B 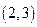 C
C 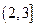 D
D 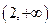
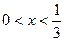 ,则
,则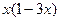 取最大值时
取最大值时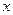 的值是( )
的值是( )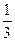

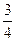
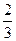
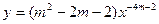 在
在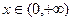 上为减函数,则实数
上为减函数,则实数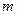 的值是__________.
的值是__________.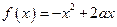 与
与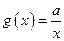 在
在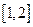 上都为减函数,则
上都为减函数,则 范围是( )
范围是( )