题目内容
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1,M是线段EF的中点.
(1)(理)求证:AM∥平面BDE;
(文)求证:AM⊥平面BDF1;
(2)求二面角A-DF-B的大小;
(3)(理)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
思路解析:本题要利用线面平行和线面垂直的判定和性质以及线线角和面面角的定义.

(1)证明:(理)如图,记AC与BD的交点为O,连结OE,
∵O、M分别是AC、EF的中点,四边形ACEF是矩形,
∴四边形AOEM是平行四边形.∴AM∥OE.
∵OE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE.
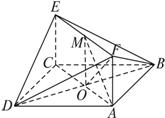
(文)如图,∵BD⊥AC,BD⊥AF,且AC交AF于A,
∴BD⊥平面AE.又∵AM![]() 平面AE,∴BD⊥AM.
平面AE,∴BD⊥AM.
∵AD=2,AF=1,OA=1,∴AOMF是正方形.
∴AM⊥OF.又AM⊥BD,且OF∩BD=O,∴AM⊥平面BDF.

(2)解:如图,在平面AFD中过A作AS⊥DF于S,连结BS,
∵AB⊥AF,AB⊥AD,AD∩AF=A,
∴AB⊥平面ADF.
∴AS是BS在平面ADF上的射影.
由三垂线定理得BS⊥DF.
∴∠BSA是二面角A-DF-B的平面角.
在Rt△ASB中,AS=![]() ,AB=
,AB=![]() ,
,
∴tan∠ASB=3,∠ASB=60°.
∴二面角A-DF-B的大小为60°.

(3)解:(理)如图,设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,AB∩AF=A,
∴PQ⊥平面ABF,QF![]() 平面ABF.
平面ABF.
∴PQ⊥QF.
在Rt△PQF中,∠FPQ=60°,PF=2PQ.
∵△PAQ为等腰直角三角形,
∴PQ=![]() (2-t).
(2-t).
又∵△PAF为直角三角形,
∴PF=![]()
∴![]() (2-t).
(2-t).
∴t=1或t=3(舍去),
即点P是AC的中点.

练习册系列答案
相关题目
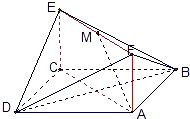 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.