题目内容
已知命题p:|2x-3|>1,命题q:log| 1 | 2 |
分析:先分别求出命题p的范围,命题q的范围,借助两个范围的大小再进行必要条件、充分条件与充要条件的判断.
解答:解:∵|2x-3|>1∴A={x|x<1或x>2}
∵log
(x2+x-5)<0
∴x2+x-5>1解得B={x|x<-3或x>2}
∵B⊆A,
∴q?p即p是q的必要不充分条件,
故答案为必要不充分.
∵log
| 1 |
| 2 |
∴x2+x-5>1解得B={x|x<-3或x>2}
∵B⊆A,
∴q?p即p是q的必要不充分条件,
故答案为必要不充分.
点评:本题主要考查了利用对数的单调性解对数不等式,以及绝对值不等式的解法和必要条件、充分条件与充要条件的判断,属于基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 p是
p是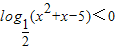 ,则¬p是¬q的 条件.
,则¬p是¬q的 条件.