题目内容
已知命题p:|2x-3|>1,命题q:log
(x2+x-5)<0,则?p是?q的
| 1 | 2 |
充分不必要
充分不必要
条件.分析:分别化简命题p,q,然后求出?p和?q,利用充分条件和必要条件的定义进行判断.
解答:解:由:|2x-3|>1,得2x-3>1或2x-3<-1,
解得x>2或x<1,
所以¬p:1≤x≤2.
由log
(x2+x-5)<0,
得x2+x-5>1,即x2+x-6>0,
解得x>2或x<-3.
所以¬q:-3≤x≤2.
所以?p是?q的充分不必要条件.
故答案为:充分不必要
解得x>2或x<1,
所以¬p:1≤x≤2.
由log
| 1 |
| 2 |
得x2+x-5>1,即x2+x-6>0,
解得x>2或x<-3.
所以¬q:-3≤x≤2.
所以?p是?q的充分不必要条件.
故答案为:充分不必要
点评:本题主要考查充分条件和必要条件的应用,以及命题的否定,比较基础.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 p是
p是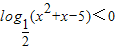 ,则¬p是¬q的 条件.
,则¬p是¬q的 条件.