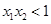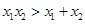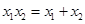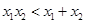题目内容
若点P是曲线y=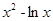 上任意一点,则点P到直线y=x-2的最小距离是 ( )
上任意一点,则点P到直线y=x-2的最小距离是 ( )
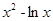 上任意一点,则点P到直线y=x-2的最小距离是 ( )
上任意一点,则点P到直线y=x-2的最小距离是 ( )A.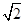 | B.1 | C. | D.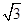 |
A
试题分析:点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
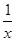 =1,x=1,或 x=-
=1,x=1,或 x=-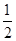 (舍去),
(舍去),故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
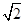 ,
,故点P到直线y=x-2的最小距离为
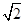 ,
,故选A.
点评:运用导数的几何意义曲线,将y=
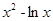 上任意一点P到直线y=x-2的最小距离计算,转化成为求两平行直线之间距离,体现了转化与化归的数学思想.
上任意一点P到直线y=x-2的最小距离计算,转化成为求两平行直线之间距离,体现了转化与化归的数学思想.
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
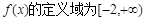 ,且
,且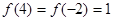 ,
,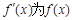 的导函数,函数
的导函数,函数 的图象如图所示.则平面区域
的图象如图所示.则平面区域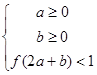 所围成的面积是( )
所围成的面积是( )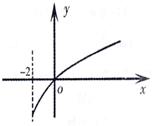
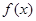 ,恒有
,恒有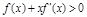 ,则
,则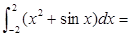 ___________.
___________.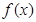

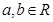
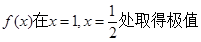 ,
,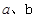 的值;
的值;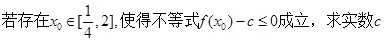 的最小值。
的最小值。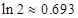 )
)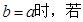
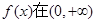 上是单调函数,求
上是单调函数,求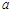 的取值范围。
的取值范围。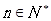 ,曲线
,曲线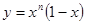 在
在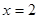 处的切线与
处的切线与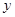 轴的交点的纵坐标为
轴的交点的纵坐标为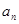 ,则
,则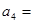 ( )
( )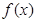 是最小正周期为
是最小正周期为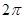 的偶函数,
的偶函数,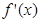 是
是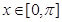 时,
时,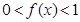 ;当
;当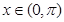 且
且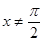 时,
时,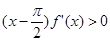 ,则函数
,则函数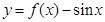 在
在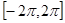 上的零点个数为
上的零点个数为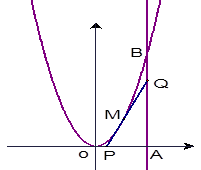
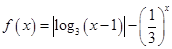 有两个零点
有两个零点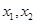 ,则( )
,则( )