题目内容
已知偶函数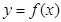 满足条件
满足条件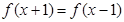 ,且当
,且当 时,
时,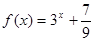 ,则
,则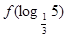 的值等于 。
的值等于 。
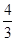
解析试题分析:因为偶函数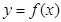 满足条件
满足条件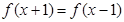 ,所以函数
,所以函数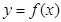 的周期为2,所以
的周期为2,所以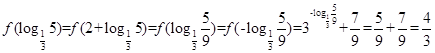 。
。
考点:函数的奇偶性;函数的周期性,;对数函数的单调性;对数的运算。
点评:本题主要考查函数的奇偶性和周期性的灵活应用。
函数周期的判断:
① 函数y="f(x),x∈R," 若f(x+a)=f(x-a),则函数的周期为2|a|;
② 函数y="f(x),x∈R," 若f(x+a)=-f(x),则函数的周期为2|a|;
③ 函数y="f(x),x∈R," 若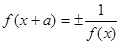 ,则函数的周期为2|a|;
,则函数的周期为2|a|;
④ 若函数 的图象同时关于直线
的图象同时关于直线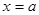 与
与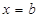 对称,那么其周期为
对称,那么其周期为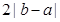 。
。

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数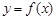 满足:①
满足:①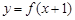 是偶函数;②在区间
是偶函数;②在区间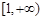 上是增函数.若
上是增函数.若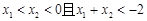 ,则
,则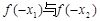 的大小关系是( )
的大小关系是( )
A.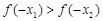 | B.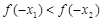 | C.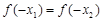 | D.无法确定 |
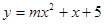 在
在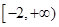 上是增函数,则
上是增函数,则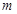 的取值范围是____________。
的取值范围是____________。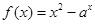 ,若对任意
,若对任意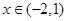 ,
,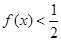 恒成立,则a的取值范围是________
恒成立,则a的取值范围是________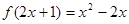 ,则
,则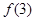 = .
= . 若
若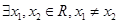 ,
,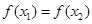 成立,则实数
成立,则实数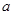 的取值范围是 。
的取值范围是 。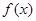 是定义域为
是定义域为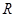 的奇函数,当
的奇函数,当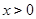 时
时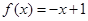 ,则当
,则当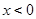 时,
时, 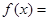
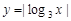 在区间
在区间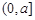 上单调递减,则实数
上单调递减,则实数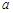 的取值范围为 .
的取值范围为 . 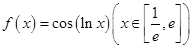 的单调递减区间是 .
的单调递减区间是 .