[题目]已知点.动圆与直线切于点.过与圆相切的两直线相交于点.则点的轨迹方程为( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知点，动圆与直线切于点，过与圆相切的两直线相交于点，则点的轨迹方程为（）

A. B.

C. D.

【答案】A

【解析】

先由题意画出图形，可见⊙C是△PMN的内切圆，则由切线长定理得|MA|=|MB|、|ND|=|NB|、|PA|=|PD|；此时求|PM|﹣|PN|可得定值，即满足双曲线的定义；然后求出a、b，写出方程即可（要注意x的取值范围）．

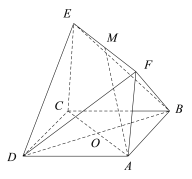
由题意画图如下

可见|MA|=|MB|=4，|ND|=|NB|=2，且|PA|=|PD|，

那么|PM|﹣|PN|=（|PA|+|MA|）﹣（|PD|+|ND|）=|MA|﹣|ND|=4﹣2=2＜|MN|，

所以点P的轨迹为双曲线的右支（右顶点除外），

又2a=2，c=3，则a=1，b2=9﹣1=8，

所以点P的轨迹方程为（x＞1）．

故选：A．

练习册系列答案

1加1阅读好卷系列答案

相关题目

【题目】如图，已知正方形和矩形所在的平面互相垂直，，，M是线段的中点.

（Ⅰ）求证：∥平面；

（Ⅱ）求证：平面；

(Ⅲ) 求点到面的距离.

【题目】已知函数f（x）=loga（x+b）（其中a，b为常数，且a＞0，a≠1）的图象经过点A（﹣2，0），B（1，2）．
（1）求f（x）的解析式；
（2）若函数g（x）=（）2x﹣（）x﹣1，x∈[0，+∞），求g（x）的值域．

【题目】已知函数f（x）=ex﹣ln（x+m）
（1）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性；
（2）当m≤2时，证明f（x）＞0．

【题目】函数f（x）=（x2﹣2x﹣3）的单调减区间是（　　）
A.（3，+∞）
B.（1，+∞）
C.（﹣∞，1）
D.（﹣∞，﹣1）

【题目】已知二次函数f（x）满足f（0）=2和f（x+1）﹣f（x）=2x﹣1对任意实数x都成立．
（1）求函数f（x）的解析式；
（2）当t∈[﹣1，3]时，求y=f（2t）的值域．

A. 有且只有一个 B. 有且只有三个 C. 有且只有四个 D. 有且只有五个

【题目】执行两次如图所示的程序框图，若第一次输入的x值为7，第二次输入的x值为9，则第一次，第二次输出的a值分别为（　　）

A.0，0
B.1，1
C.0，1
D.1，0

销售经验x/年	1	3	4	4	6	8	10	10	11	13
年销售额y/千元	80	97	92	102	103	111	119	123	117	136

(1)依据这些数据画出散点图并作直线＝78＋4.2x，计算；

(2)依据这些数据求回归直线方程并据此计算；

(3)比较(1) (2)中的残差平方和的大小.

试题分类