题目内容
18.已知函数f(x)=$\left\{{\begin{array}{l}{-{x^2}+x+k,x≤1}\\{-\frac{1}{2}+{{log}_{\frac{1}{3}}}x,x>1}\end{array}}$,g(x)=$\frac{x}{{{x^2}+1}}$(a∈R),若对任意的x1,x2∈{x|x∈R,x>-2},均有f(x1)≤g(x2),则实数k的取值范围是$({-∞,-\frac{3}{4}}]$.分析 对任意的x1,x2∈R,均有f(x1)≤g(x2)可化为f(x)max≤g(x)min,由基本不等式可知g(x)min=-$\frac{1}{2}$;再分段讨论确定函数f(x)可能的最大值,从而可得$\frac{1}{4}$+k≤-$\frac{1}{2}$,从而解得实数k的取值范围.
解答 解:若对任意的x1,x2∈R,均有f(x1)≤g(x2),
则f(x)max≤g(x)min,
对于函数f(x),当-2<x≤1时,f(x)=-x2+x+k=$-(x-\frac{1}{2})^{2}+\frac{1}{4}+k$≤$\frac{1}{4}+k$;当x>1时,f(x)=-$\frac{1}{2}$+$lo{g}_{\frac{1}{3}}x$$<-\frac{1}{2}$.
当$k≤-\frac{3}{4}$时,$\frac{1}{4}+k$≤$-\frac{1}{2}$,∴f(x)<$-\frac{1}{2}$;
当$k>-\frac{3}{4}$时,$\frac{1}{4}+k$>$-\frac{1}{2}$,∴f(x)max=$\frac{1}{4}+k$.
当x=0时,g(x)=0,当x>0时,g(x)>0,
当x<0时,g(x)<0,
故g(x)min在(-∞,0)上取得,
当x<0时,g(x)=$\frac{x}{{x}^{2}+1}$=$\frac{1}{x+\frac{1}{x}}$≥$\frac{1}{-2}=-\frac{1}{2}$(当且仅当x=-1时,等号成立).
故g(x)min=-$\frac{1}{2}$.
由$\frac{1}{4}+k≤-\frac{1}{2}$,解得k$≤-\frac{3}{4}$.
∴实数k的取值范围是$({-∞,-\frac{3}{4}}]$.
故答案为:$({-∞,-\frac{3}{4}}]$.
点评 本题考查了分段函数的应用,考查基本不等式在求最值中的应用,同时考查了恒成立问题,属于中档题.

| A. | 假设n=k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| B. | 假设n≥k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| C. | 假设n=2k+1(k∈N*)时命题成立,即x2k+1+y2k+1能被x+y整除 | |
| D. | 假设n=2k-1(k∈N*)时命题成立,即x2k-1+y2k-1能被x+y整除 |
| A. | M2≥2n+1 | B. | 当n≥2时,2M≥4n-2 | C. | M2≥2n+1 | D. | 当n≥3时,2M≥2n+2 |
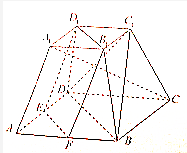 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.