题目内容
10.有一个圆锥,其母线长为18cm,要使其体积最大,则该圆锥的高为( )| A. | 8cm | B. | 6$\sqrt{3}$cm | C. | 8$\sqrt{3}$cm | D. | 12cm |
分析 设圆锥的底面半径为r,高为h,表示出圆锥的体积,利用但是判断函数的单调性求出函数的最大值点即可.
解答 解:设圆锥的底面半径为r,高为h,则r2+h2=182,即r2=324-h2,
圆锥的体积为:V=$\frac{1}{3}$πr2h=$\frac{1}{3}$π(324h-h3).(0<h<18).
∴V′=$\frac{1}{3}$π(324-3h2)=π(108-h2),
令V′=0,则h=6$\sqrt{3}$,
∵0<h<6$\sqrt{3}$时,V′>0,6$\sqrt{3}$<h<18时,V′<0,
故h=6$\sqrt{3}$时,V取最大值,
故选:B
点评 本题考查函数与方程的综合应用,函数的导数求解函数的最值的基本方法,考查计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≥2\\ x≥0,y≥0\end{array}\right.$则z=x+5y的最小值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
2.设点M(1,y0),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则y0的取值范围是( )
| A. | [-1,1] | B. | [-$\frac{1}{2},\frac{1}{2}$] | C. | [-$\sqrt{2},\sqrt{2}$] | D. | [-$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$] |
19.以下各点中,在不等式组$\left\{\begin{array}{l}{x-2y+5>0}\\{x-y+3≤0}\end{array}\right.$表示的平面区域中的点是( )
| A. | (-2,1) | B. | (2,1) | C. | (-1,2) | D. | (1,2) |
17.当直线y=kx与曲线y=|x|-|x-2|有3个公共点时,实数k的取值范围是( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
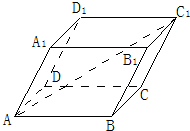 已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.
已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.