题目内容
过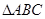 所在平面
所在平面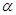 外一点
外一点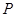 ,作
,作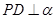 ,垂足为D,若
,垂足为D,若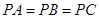 ,则D是
,则D是 的 心.(从外心,内心,重心,垂心中选一个)
的 心.(从外心,内心,重心,垂心中选一个)
 所在平面
所在平面 外一点
外一点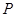 ,作
,作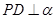 ,垂足为D,若
,垂足为D,若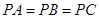 ,则D是
,则D是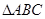 的 心.(从外心,内心,重心,垂心中选一个)
的 心.(从外心,内心,重心,垂心中选一个)外
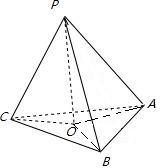
点P为△ABC所在平面外一点,PO⊥α,垂足为O,若PA=PB=PC,可证得△POA≌△POB≌△POC,从而证得OA=OB=OC,符合这一性质的点O是△ABC外心
证明:点P为△ABC所在平面外一点,PO⊥α,垂足为O,若PA=PB=PC,
故△POA,△POB,△POC都是直角三角形
∵PO是公共边,PA=PB=PC
∴△POA≌△POB≌△POC
∴OA=OB=OC
故O是△ABC外心
故答案为:外.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的外接圆半径为
的外接圆半径为 ,内切圆半径为
,内切圆半径为 ,求证:
,求证: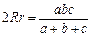 .
.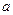 、
、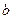 、
、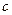 ,设向量
,设向量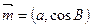 ,
,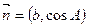 ,且
,且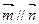 ,
,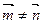 .
.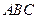 是直角三角形;
是直角三角形;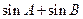 的取值范围.
的取值范围. ,c=2,B=150°,求边b的长及S△。
,c=2,B=150°,求边b的长及S△。 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为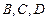 ).当返回舱距地面1万米的
).当返回舱距地面1万米的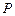 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在 点着陆),
点着陆),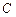 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为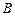 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西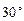 方向,仰角为
方向,仰角为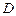 救援中心测得着陆点
救援中心测得着陆点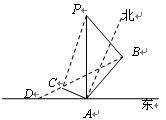
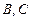
 两救援中心间的距离;
两救援中心间的距离; 中,角
中,角 ,
,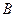 ,
,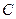 所对的边分别为
所对的边分别为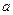 ,
,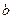 ,
,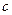 ,且
,且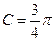 ,
,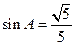 .
.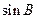 的值;
的值;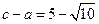 ,求
,求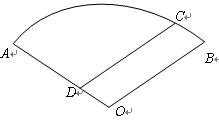
 中,角A,B,C,所对的边分别是
中,角A,B,C,所对的边分别是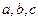 ,且
,且 ;
;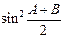
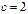 ,求
,求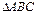 面积的最大值。
面积的最大值。 中,角
中,角 的对边分别为
的对边分别为 ,下列四个命题
,下列四个命题 ,则
,则 ;②若
;②若 ,则满足条件的三角形共有两个;③若
,则满足条件的三角形共有两个;③若 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 ,则
,则 .其中正确命题的个数是( )
.其中正确命题的个数是( )