题目内容
在区间[-π,π]内随机取两个数分别为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为( )
A.1-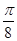 | B.1-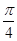 | C.1-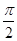 | D.1-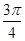 |
B
函数f(x)=x2+2ax-b2+π2有零点,需Δ=4a2-4(-b2+π2)≥0,即a2+b2≥π2成立.而a,b∈[-π,π],建立平面直角坐标系,满足a2+b2≥π2的点(a,b)如图阴影部分所示,
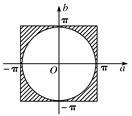
所求事件的概率为P=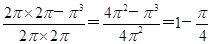 ,故选B.
,故选B.

所求事件的概率为P=
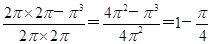 ,故选B.
,故选B.
练习册系列答案
相关题目
 的线段
的线段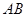 上任取一点
上任取一点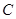 ,现作一矩形,邻边长分别等于线段
,现作一矩形,邻边长分别等于线段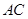 ,
,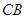 的长,则该矩形面积大于
的长,则该矩形面积大于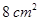 的概率为 .
的概率为 . S△ABC的概率是( )
S△ABC的概率是( )




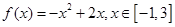 ,则任取一点
,则任取一点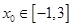 ,使得
,使得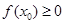 的概率为
的概率为 



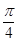 B.
B. 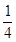 C.
C. 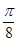 D.
D. 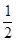
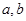 满足
满足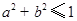 ,则关于
,则关于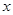 的方程
的方程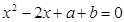 有实数根的概率是_______________.
有实数根的概率是_______________.