题目内容
1.(理)已知△ABC中,若sinA=m,sinB=n,当m、n满足条件m、n有且只有一个为1时(只需写出满意的一个条件),cosC具有唯一确定的值.分析 由题意和正弦定理可得$\frac{sinA}{a}$=$\frac{sinB}{b}$=$\frac{sinC}{c}$=k,可得a=$\frac{m}{k}$,b=$\frac{n}{k}$,c=$\frac{sinC}{k}$,代入余弦定理可得2abcodC=a2+b2-c2,由关于cosC的二次方程有唯一的解可得.
解答 解:∵△ABC中sinA=m,sinB=n,
由正弦定理可得$\frac{sinA}{a}$=$\frac{sinB}{b}$=$\frac{sinC}{c}$=k,
∴a=$\frac{m}{k}$,b=$\frac{n}{k}$,c=$\frac{sinC}{k}$,
再由余弦定理可得2abcodC=a2+b2-c2,
∴$\frac{2mn}{{k}^{2}}$cosC=$\frac{{m}^{2}}{{k}^{2}}$+$\frac{{n}^{2}}{{k}^{2}}$-$\frac{si{n}^{2}C}{{k}^{2}}$=$\frac{{m}^{2}+{n}^{2}-(1-co{s}^{2}C)}{{k}^{2}}$,
∴2mncosC=m2+n2-1+cos2C,即cos2C-2mncosC+(m2+n2-1)=0,
由cosC具有唯一确定的值可得△=4m2n2-4(m2+n2-1)=0,
整理可得(m2-1)(n2-1)=0,m、n不可能同时为1,
∴当m、n有且只有一个为1即该三角形为直角三角形时,cosC具有唯一确定的值.
故答案为:m、n有且只有一个为1
点评 本题考查解三角形,涉及正余弦定理和一元二次方程根的存在性,属中档题.

练习册系列答案
相关题目
11.已知A(1,0),$B(1,\sqrt{2})$将线段OA,AB各n等分,设OA上从左至右的第k个分点为Ak,AB上从下至上的第k个分点Bk(1<k<n),过点Ak且垂直于x轴的直线为lK,OBK交lK于PK,则点PK在同一( )
| A. | 圆上 | B. | 椭圆上 | C. | 双曲线上 | D. | 抛物线上 |
6.(文)已知a2+$\frac{1}{4}$c2-3=0,则c+2a的最大值是( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{7}$ | D. | 3$\sqrt{3}$ |
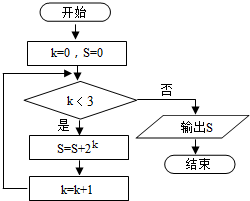
13.执行如图所示的程序框图,ze输出S的值为( )


| A. | 10 | B. | -6 | C. | 3 | D. | 12 |
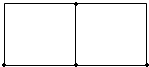 某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?
某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?